2021-2022學年福建省三明市寧化縣七年級（下）期中數學試卷

一、選擇題（本大題共10小題，共40分）

• 1．下列運算正確的是（　　）

  A．a2+a2=a4

  B．a3?a4=a12

  C．（a3）4=a12

  D．（ab）2=ab2
  組卷：266引用：5難度：0.8

  解析

• 2．我們知道，圓的周長公式是：C=2πr,那么在這個公式中，以下關于變量和常量的說法正確的是（　　）

  A．2π是常量，C，r是變量	B．2是常量，C，π，r是變量
  C．2是常量，r是變量	D．2是常量，C，r是變量
  組卷：60引用：4難度：0.7

  解析

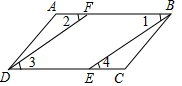• 3．如圖，點F，E分別在線段AB和CD上，下列條件能判定AB∥CD的是（　　）

  A．∠1=∠2

  B．∠1=∠4

  C．∠4=∠2

  D．∠3=∠4
  組卷：1336引用：23難度：0.9

  解析

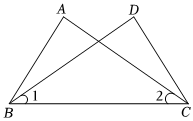• 4．如圖，已知∠ABC=∠DCB，添加下列條件，不能使△ABC≌△DCB的是（　　）

  A．AC=DB

  B．AB=DC

  C．∠A=∠D

  D．∠1=∠2
  組卷：642引用：11難度：0.7

  解析

• 5．下列各式中，不能用平方差公式計算的是（　　）

  A．（x-2y）（2y+x）	B．（x-2y）（-x-2y）
  C．（x+2y）（-x-2y）	D．（2y-x）（-x-2y）
  組卷：182引用：3難度：0.8

  解析

• 6．若∠α與∠β是內錯角，且∠α=50°，則∠β的度數為（　　）

  A．50°

  B．130°

  C．50°或130°

  D．無法確定
  組卷：422引用：15難度：0.9

  解析

• 7．在某次實驗中，測得兩個變量m和v之間的4組對應數據如下表

  m	1	2	3	4
  v	2.01	4.9	10.03	17.1

  則m與v之間的關系最接近于下列各關系式中的（　　）

  A．v=2m

  B．v=m2+1

  C．v=3m-1

  D．v=3m+1
  組卷：937引用：9難度：0.9

  解析

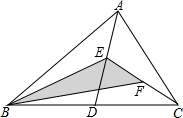• 8．如圖，在△ABC中，已知點D，E，F分別是BC，AD，CE的中點，且△ABC的面積為16，則△BEF的面積是（　　）

  A．2

  B．4

  C．6

  D．8
  組卷：4390引用：21難度：0.5

  解析

三、解答題（本大題共9小題，共86分）

• 24．閱讀以下材料：
  對數的創始人是蘇格蘭數學家納皮爾（J．Napier,1550～1617年），納皮爾發明對數是在指數書寫方式之前，直到18世紀瑞士數學家歐拉（Euler,1707～1783年）才發現指數與對數之間的聯系．
  對數的定義：一般地，若a^x=N（a＞0，a≠1），則x叫做以a為底N的對數，記作x=log_aN．如指數式2⁴=16可以轉化為4=log₂16，對數式2=log₅25可以轉化為5²=25．我們根據對數的定義可得到對數的一個性質：
  log_a（M?N）=log_aM+log_aN（a＞0，a≠1，M＞0，N＞0）．
  理由如下：設log_aM=m,log_aN=n,則M=a^m，N=aⁿ．
  ∴M?N=a^m?aⁿ=a^m+n．
  由對數的定義，得m+n=log_a（M?N）．
  又∵m+n=log_aM+log_aN，
  ∴log_a（M?N）=log_aM+log_aN．
  解答下列問題：
  （1）將指數式3⁴=81轉化為對數式：

  ；
  （2）求證：

  log

  a

  M

  N

  =

  log

  a

  M

  -

  log

  a

  N

  （

  a

  ＞

  0

  ，

  a

  ≠

  1

  ，

  M

  ＞

  0

  ，

  N

  ＞

  0

  ）

  ；
  （3）拓展運用：計算：log₈32+log₈4-log₈2．
  組卷：131引用：1難度：0.5

  解析

• 25．（1）某學習小組在探究三角形全等時，發現了下面這種典型的基本圖形．如圖1，已知：在△ABC中，∠BAC=90°，AB=AC，直線l經過點A，BD⊥直線l,CE⊥直線l,垂足分別為點D、E．證明：DE=BD+CE．
  （2）組員小劉想，如果三個角不是直角，那結論是否會成立呢？如圖2，將（1）中的條件改為：在△ABC中，AB=AC，D、A、E三點都在直線l上，并且有∠BDA=∠AEC=∠BAC=α，其中α為任意銳角或鈍角．請問結論DE=BD+CE是否成立？如成立，請你給出證明；若不成立，請說明理由．
  （3）數學老師贊賞了他們的探索精神，并鼓勵他們運用這個知識來解決問題：如圖3，過△ABC的邊AB、AC向外作正方形ABDE和正方形ACFG，AH是BC邊上的高，延長HA交EG于點I，求證：I是EG的中點．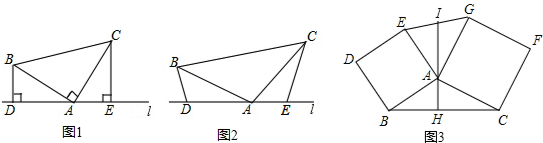
  
  組卷：13382引用：41難度：0.3

  解析