2022年山西省呂梁市孝義市中考數學三模試卷

一、選擇題（本大題共10個小題，每小題3分，共30分。在每小題給出的四個選項中，只有一項符合題目要求，請選出并在答題卡上將該選項涂黑）

• 1．-2的相反數是（　　）

  A．2

  B．-2

  C． 1 2

  D．±2
  組卷：297引用：17難度：0.9

  解析

• 2．如圖，直線a,b被直線c所截，且a∥b,∠1=55°，則∠2等于（　　）

  A．55°

  B．65°

  C．125°

  D．135°
  組卷：287引用：7難度：0.7

  解析

• 3．一季度，面對國際環境更趨復雜嚴峻和國內疫情頻發帶來的多重考驗，在以習近平同志為核心的黨中央堅強領導下，科學統籌疫情防控和經濟社會發展，初步核算，一季度國內生產總值約為27萬億元，按不變價格計算，同比增長4.8%．數據27萬億元用科學記數法表示為（　　）

  A．2.7×1013元	B．2.7×1014元
  C．0.27×1014元	D．27×1012元
  組卷：45引用：2難度：0.7

  解析

• 4．如圖是一個正方體的表面展開圖，在原正方體中，與“誠”字所在面相對的面上的漢字是（　　）

  A．守

  B．信

  C．擔

  D．當
  組卷：167引用：4難度：0.8

  解析

• 5．為了防控疫情，各級防控部門積極推廣疫苗接種工作，某市某接種點1-5月接種人數如表，則這組數據的中位數和眾數分別是（　　）

  月份	1	2	3	4	5
  接種人數（萬人）	1.2	1.8	1.6	2.1	1.8

  A．1.2萬人，1.6萬人	B．1.6萬人，1.8萬人
  C．1.8萬人，1.8萬人	D．1.8萬人，2.1萬人
  組卷：108引用：3難度：0.6

  解析

• 6．一元二次方程2x²-3x-2=0的根為（　　）

  A．x1=2，x2= 1 2	B．x1=-2，x2=- 1 2
  C．x1=-2，x2= 1 2	D．x1=2，x2=- 1 2
  組卷：171引用：2難度：0.9

  解析

• 7．公元前6世紀古希臘的畢達哥拉斯學派有一種觀點，即“萬物皆數”，一切量都可以用整數或整數比（分數）表示，后來，當這一學派中的希帕索斯發現，邊長為1的正方形的對角線的長度不能用整數或整數的比表示時，畢達哥拉斯學派感到驚恐不安，由此，引發了第一次數學危機，這兒“不能用整數或整數的比表示的數”指的是（　　）

  A．有理數

  B．無理數

  C．合數

  D．質數
  組卷：116引用：8難度：0.9

  解析

三、解答題（本大題共8個小題，共75分。解答題應寫出文字說明、證明過程或演算步驟）

• 22．綜合與實踐
  數學活動課上，老師讓同學們根據下面情境提出問題并解答．
  問題情境：在?ABCD中，點P是邊AD上一點．將△PDC沿直線PC折疊，點D的對應點為E．
  “興趣小組”提出的問題是：如圖1，若點P與點A重合，過點E作EF∥AD，與PC交于點F，連接DF，則四邊形AEFD是菱形．
  數學思考：
  （1）請你證明“興趣小組”提出的問題；
  拓展探究：
  （2）“智慧小組”提出的問題是：如圖2，當點P為AD的中點時，延長CE交AB于點F，連接PF．試判斷PF與PC的位置關系，并說明理由．
  請你幫助他們解決此問題．
  問題解決：
  “創新小組”在前兩個小組的啟發下，提出的問題是：如圖3，當點E恰好落在AB邊上時，AP=3，PD=4，DC=10．則AE的長為

  ．（直接寫出結果）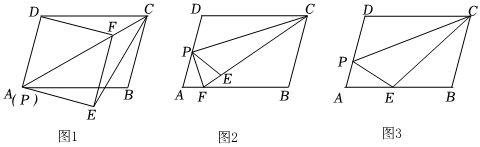
  
  組卷：510引用：5難度：0.1

  解析

• 23．綜合與探究
  如圖，拋物線y=-

  2

  9

  x²+

  2

  3

  x+4與x軸交于A，B兩點，與y軸交于點C．點M是y軸右側拋物線上一動點，過點M作AC的平行線，交直線BC于點D，交x軸于點E．
  （1）請直接寫出點A，B，C的坐標及直線BC的解析式；
  （2）當DE=OE時，求點D的坐標；
  （3）試探究在點M運動的過程中，是否存在以點A，C，E，M，為頂點的四邊形是平行四邊形？若存在，直接寫出M的坐標，若不存在說明理由．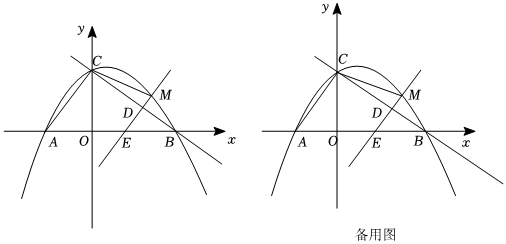
  
  組卷：142引用：1難度：0.1

  解析