2022-2023學年浙江省衢州市柯城區興華中學九年級（下）月考數學試卷（3月份）

一、選擇題（本大題共有10小題，每小題3分，共30分，請選出一個符合題意的正確的選項填涂在答題卷內，不選、多選、錯選均不給分）

• 1．下列各式，結果等于2的是（　　）

  A．0-2

  B．-（-2）

  C．-|2|

  D．-|-2|
  組卷：114引用：2難度：0.9

  解析

• 2．下列圖形，屬于中心對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：74引用：3難度：0.9

  解析

• 3．小明同學在“百度”搜索引擎中輸入“2023亞運會”，搜索到與之相關的結果條數為31400000，這個數用科學記數法表示為（　　）

  A．31.4×106

  B．3.14×108

  C．0.314×107

  D．3.14×107
  組卷：54引用：6難度：0.9

  解析

• 4．下列計算正確的是（　　）

  A．2a2-a2=1	B．（a2）3=a5
  C．a6÷a2=a4	D．（a+b）2=a2+b2
  組卷：46引用：1難度：0.8

  解析

• 5．在一個不透明的袋子中裝有5個紅球和3個黑球，它們除顏色外其他均相同，從中任意摸出一個球，則摸出黑球的概率是（　　）

  A． 1 8

  B． 3 8

  C． 1 2

  D． 5 8
  組卷：71引用：5難度：0.8

  解析

• 6．“今有人盜庫絹，不知所失幾何．但聞草中分絹，人得六匹，盈六匹；人得七匹，不足七匹，問人、絹各幾何？（選自《孫子算經》）”．大意為：有盜賊竊去庫存的綢緞，不知究竟竊去多少．有人在草叢中聽到這幫盜賊分贓的情況．如果每個盜賊分得6匹，就多出6匹；如果每個盜賊分得7匹，就缺少7匹．盜賊有幾人？失竊的綢緞有幾匹？設盜賊有x人，失竊的綢緞有y匹，根據題意可列方程組為（　　）

  A． 6 x + 6 = y 7 x + 7 = y	B． 6 x + 6 = y 7 x - 7 = y
  C． 6 x - 6 = y 7 x + 7 = y	D． 6 x - 6 = y 7 x - 7 = y
  組卷：826引用：11難度：0.7

  解析

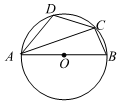• 7．如圖，AB是⊙O的直徑，點C，D為⊙O上的點．若∠D=120°，則∠CAB的度數為（　　）

  A．30°

  B．40°

  C．50°

  D．60°
  組卷：1200引用：12難度：0.5

  解析

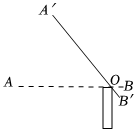• 8．如圖，某停車場入口的欄桿從水平位置AB繞點O旋轉到A′B′的位置．已知AO=4米，若欄桿的旋轉角∠AOA′=50°，則欄桿端點A上升的垂直距離A′H為（　　）

  A．4sin50°米

  B．4cos50°米

  C．4tan50°米

  D． 4 sin 50 ° 米
  組卷：70引用：1難度：0.5

  解析

三、解答題（本大題共8小題，共計66分）

• 23．根據素材解決問題．
  

  設計貨船通過圓形拱橋的方案
  素材1	圖1中有一座圓拱石橋，圖2是其圓形橋拱的示意圖，測得水面寬AB=16m,拱頂離水面的距離CD=4m.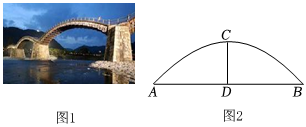
  素材2	如圖3，一艘貨船露出水面部分的橫截面為矩形EFGH，測得EF=3m,EH=10m.因水深足夠，貨船可以根據需要運載貨物．據調查，船身下降的高度y（米）與貨船增加的載重量x（噸）滿足函數關系式 y = 1 100 x ．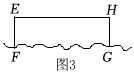
  問題解決
  任務1	確定橋拱半徑	求圓形橋拱的半徑
  任務2	擬定設計方案	根據圖3狀態，貨船能否通過圓形拱橋？若能，最多還能卸載多少噸貨物？若不能，至少要增加多少噸貨物才能通過？
  組卷：2018引用：15難度：0.4

  解析

• 24．在四邊形ABCD中，AC與BD互相垂直且平分．
  【推理探究】（1）如圖1，已知AC=BD，點E是線段OA上任意一點，CF⊥BE交OB于點G，垂足為點F，求證：OE=OG．
  【類比應用】（2）如圖2，已知AC=BD，點E在OA的延長線上，且OA：AE=2：1，CF⊥BE交OB的延長線于點G，AB=8，求tan∠ABE的值．
  【拓展延伸】（3）如圖3，已知∠BAD=60°，點E是OA的三等分點，CF⊥BE交直線OB于點G，垂足為點F，AB=8，求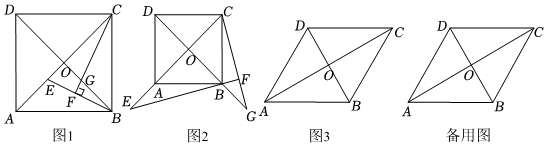

  OG

  CF

  的值．
  
  組卷：159引用：2難度：0.1

  解析