2022-2023學年河南省駐馬店市汝南縣七年級(下)期中數學試卷
發布:2024/7/5 8:0:9
一、選擇題(每小題3分,共30分)
-
1.如圖所示的四個圖形中,∠1和∠2一定相等的是( )
A. 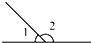
B. 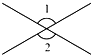
C. 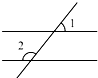
D. 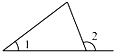 組卷:171引用:3難度:0.9
組卷:171引用:3難度:0.9 -
 2.近段時間,以熊貓為原型的2022北京冬奧會吉祥物“冰墩墩”成了全網“頂流”.如圖,通過平移如圖吉祥物“冰墩墩”可以得到的圖形是( )
2.近段時間,以熊貓為原型的2022北京冬奧會吉祥物“冰墩墩”成了全網“頂流”.如圖,通過平移如圖吉祥物“冰墩墩”可以得到的圖形是( )A. 
B. 
C. 
D.  組卷:858引用:33難度:0.9
組卷:858引用:33難度:0.9 -
3.下列式子正確的是( )
A.± =±39B. =23-8C. =-3(-3)2D.± =24組卷:103引用:2難度:0.9 -
4.在平面直角坐標系中,下面的點在第一象限的是( )
A.(1,2) B.(-2,3) C.(0,0) D.(-3,-2) 組卷:126引用:13難度:0.9 -
5.下列命題中,是真命題的是( )
A.鄰補角是互補的角 B.兩個銳角的和是銳角 C.相等的角是對頂角 D.同旁內角互補 組卷:173引用:5難度:0.6 -
6.在平面直角坐標系中,將點A(-1,-7)向右平移3個單位長度,再向上平移4個單位長度后與點B重合,則點B的坐標是( )
A.(2,-3) B.(2,-10) C.(-4,-3) D.(-4,3) 組卷:48引用:2難度:0.5 -
 7.如圖,點E在AC的延長線上,下列條件不能判斷AC∥BD的是( )
7.如圖,點E在AC的延長線上,下列條件不能判斷AC∥BD的是( )A.∠3=∠4 B.∠D=∠DCE C.∠1=∠2 D.∠D+∠ACD=180° 組卷:899引用:29難度:0.9
三、解答題(共70分)
-
22.本學期我們在第六章《實數》中學習了平方根和立方根.如表是平方根和立方根的部分內容.通過類比平方根和立方根的有關內容可以了解有關四次方根的知識請仔細閱讀下表并解決下列問題:
(1)類比平方根和立方根的定義,給四次方根下定義:平方根 立方根 定義 一般地,如果一個數的平方等于a,那么這個數叫做a的平方根或二次方根.這就是說,如果x2=a,那么x叫做a的平方根. 一般地,如果一個數的立方等于a,那么這個數叫做a的立方根或三次方根.這就是說,如果x3=a,那么x叫做a的立方根. 運算 求一個數a的平方根的運算,叫做開平方.開平方與平方互為逆運算. 求一個數a的立方根的運算,叫做開立方.開立方與立方互為逆運算. 特征 正數有兩個平方根,它們互為相反數;0的平方根是0;負數沒有平方根. 正數的立方根是正數;
0的立方根是0;
負數的立方根是負數.表示與讀法 正數a的平方根可以用“± ”表示,讀作“正負根號a”.a一個數a的立方根可以用“ ”表示,讀作“三次根號a”.3a
一般地,,那么x叫作a的四次方根.
(2)思考與歸納
求一個數a的四次方根的運算叫做開四次方.開四次方和四次方互為逆運算.
①探究:
81的四次方根是 ;
0的四次方根是 ;
-4 (填“有”或“沒有”)四次方根.
②歸納:
根據上述①中情況,類比平方根和立方根的特征,歸納四次方根的特征:;
③總結:
我們歸納四次方根的特征時,分了正數、0、負數三類進行研究,這種思想叫 ;
四次方根的特征是由81,,0等這幾個特殊數的四次方根的特征歸納出來的,這種思想叫 (填正確選項的代碼).1681
A.類比思想
B.分類討論思想
C.由一般到特殊的思想
D.由特殊到一般的思想
(3)鞏固與應用
①±= (將結果直接填到橫線上).4256
②比較大小:3(填“>”或“=”或“<”).416組卷:130引用:1難度:0.5 -
23.【問題背景】
同學們,我們一起觀察小豬的豬蹄,你會發現一個我們熟悉的幾何圖形,我們就把這個圖形象的稱為“豬蹄模型”,豬蹄模型中蘊含著角的數量關系.
(1)如圖1,AB∥CD,E為AB,CD之間一點,連接BE,DE,得到∠BED.試探究∠BED與∠B、∠D之間的數量關系,并說明理由.
(2)【類比探究】請你利用上述“豬蹄模型”得到的結論或解題方法,完成下面的問題:
如圖2,已知MN∥PQ,CD∥AB,點E在PQ上,∠ECN=∠CAB,請你說明∠ABP+∠DCE=∠CAB;(把下面的解答補充完整)
解:因為CD∥AB
所以∠CAB+=180°( )
因為∠ECM+∠ECN=180°( )
又因為∠ECN=∠CAB
所以∠=∠( )
即∠MCA+∠ACE=∠DCE+∠ACE
所以∠MCA=∠DCE
由(1)知∠MCA+∠ABP=∠CAB
∴∠ABP+∠DCE=∠CAB
(3)【拓展延伸】如圖3,BF平分∠ABP,CG平分∠ACN,AF∥CG.若∠CAB=68°,請直接寫出∠AFB的度數為 .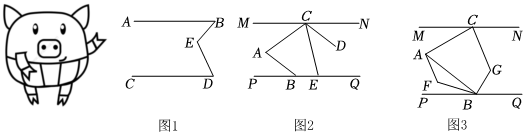 組卷:2375引用:8難度:0.3
組卷:2375引用:8難度:0.3


