2021-2022學(xué)年山東省臨沂市費(fèi)縣一中八年級(jí)（下）期中數(shù)學(xué)試卷

一、單選題。

• 1．當(dāng)

  a

  +

  2

  a

  -

  2

  有意義時(shí)，a的取值范圍是（　　）

  A．a(chǎn)≥2

  B．a(chǎn)＞2

  C．a(chǎn)≠2

  D．a(chǎn)≠-2
  組卷：476引用：33難度：0.9

  解析

• 2．下列式子中，最簡(jiǎn)二次根式的是（　　）

  A． 1 2

  B． 5

  C． 12

  D． 4
  組卷：167引用：6難度：0.7

  解析

• 3．在以O(shè)為坐標(biāo)原點(diǎn)的平面直角坐標(biāo)系中，點(diǎn)P（-2，1）到坐標(biāo)原點(diǎn)O的距離為（　　）

  A．- 5

  B． 5

  C．2

  D．5
  組卷：77引用：2難度：0.8

  解析

• 4．某公園的A，B，C處分別有海盜船、摩天輪、旋轉(zhuǎn)木馬三個(gè)娛樂(lè)項(xiàng)目，現(xiàn)要在公園內(nèi)一個(gè)售票中心，使三個(gè)娛樂(lè)項(xiàng)目所處位置到售票中心的距離相等，則售票中心應(yīng)建立在（　　）

  A．△ABC三邊高線的交點(diǎn)處

  B．△ABC三角角平分線的交點(diǎn)處

  C．△ABC三邊中線的交點(diǎn)處

  D．△ABC三邊垂直平分線的交點(diǎn)處
  組卷：562引用：9難度：0.5

  解析

• 5．若x₁，x₂是方程x²+bx-3b=0的兩個(gè)根，且

  x

  1

  2

  +

  x

  2

  2

  =

  7

  ，則b的值是（　　）

  A．1

  B．-7

  C．1或7

  D．7或-1
  組卷：233引用：7難度：0.6

  解析

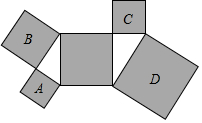• 6．如圖，所有陰影部分四邊形都是正方形，所有三角形都是直角三角形，若正方形A、B、D的面積依次為6、10、24，則正方形C的面積為（　　）

  A．4

  B．6

  C．8

  D．12
  組卷：2145引用：21難度：0.7

  解析

• 7．一根長(zhǎng)18cm的牙刷置于底面直徑為5cm、高為12cm的圓柱形水杯中，牙刷露在杯子外面的長(zhǎng)度為h cm,則h的取值范圍是（　　）

  A．5＜h≤6

  B．6＜h≤7

  C．5≤h≤6

  D．5≤h＜6
  組卷：29引用：3難度：0.5

  解析

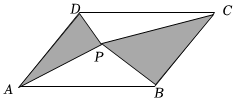• 8．如圖，P是面積為S的平行四邊形ABCD內(nèi)任意一點(diǎn)，△PAD的面積為S₁，△PBC的面積為S₂，則（　　）

  A． S 1 + S 2 ＞ s 2

  B． S 1 + S 2 ＜ s 2

  C． S 1 + S 2 = s 2

  D．S1+S2的大小與P點(diǎn)位置有關(guān)
  組卷：828引用：9難度：0.5

  解析

三、解答題。

• 24．勾股定理是一個(gè)基本的幾何定理，早在我國(guó)西漢時(shí)期算書《周髀算經(jīng)》就有“勾三股四弦五”的記載．如果一個(gè)直角三角形三邊長(zhǎng)都是正整數(shù)，這樣的直角三角形叫做“整數(shù)直角三角形”；這三個(gè)整數(shù)叫做一組“勾股數(shù)”．在一次“構(gòu)造勾股數(shù)”的探究性學(xué)習(xí)中，老師給出了下表：
  

  m	2	3	3	4	…
  n	1	1	2	3	…
  a	22+12	32+12	32+22	42+32	…
  b	4	6	12	24	…
  c	22-12	32-12	32-22	42-32	…

  其中m、n為正整數(shù)，且m＞n.
  （1）觀察表格，當(dāng)m=2，n=1時(shí)，此時(shí)對(duì)應(yīng)的a、b、c的值能否為直角三角形三邊的長(zhǎng)？說(shuō)明你的理由．
  （2）探究a,b,c與m、n之間的關(guān)系并用含m、n的代數(shù)式表示：a=

  ，b=

  ，c=

  ．
  （3）以a,b,c為邊長(zhǎng)的三角形是否一定為直角三角形？如果是，請(qǐng)說(shuō)明理由；如果不是，請(qǐng)舉出反例．
  組卷：211引用：8難度：0.6

  解析

• 25．綜合與探究
  問(wèn)題情境：
  在綜合實(shí)踐課上，李老師讓同學(xué)們根據(jù)如下問(wèn)題情境，寫出兩個(gè)數(shù)學(xué)結(jié)論：如圖（1），正方形ABCD的對(duì)角線交于點(diǎn)O，點(diǎn)O又是正方形OEFG的一個(gè)頂點(diǎn)（正方形OEFG的邊長(zhǎng)足夠長(zhǎng)），將正方形OEFG繞點(diǎn)O做旋轉(zhuǎn)實(shí)驗(yàn)，OE與BC交于點(diǎn)M，OG與DC交于點(diǎn)N．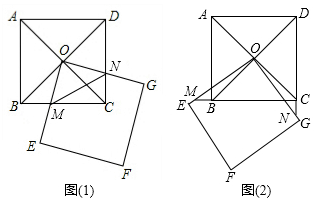
  
  “興趣小組”寫出的兩個(gè)數(shù)學(xué)結(jié)論是：
  ①S_△OMC+S_△ONC=

  1

  4

  S_{正方形ABCD}；
  ②BM²+CM²=2OM²．
  問(wèn)題解決：
  （1）請(qǐng)你證明“興趣小組”所寫的兩個(gè)結(jié)論的正確性．
  類比探究：
  （2）解決完“興趣小組”的兩個(gè)問(wèn)題后，老師讓同學(xué)們繼續(xù)探究，再提出新的問(wèn)題；“智慧小組“提出的問(wèn)題是：如圖（2），將正方形OEFG在圖（1）的基礎(chǔ)上旋轉(zhuǎn)一定的角度，當(dāng)OE與CB的延長(zhǎng)線交于點(diǎn)M，OG與DC的延長(zhǎng)線交于點(diǎn)N，則“興趣小組”所寫的兩個(gè)結(jié)論是否仍然成立？請(qǐng)說(shuō)明理由．
  組卷：245引用：5難度：0.2

  解析