當前位置：
章節挑題
請展開查看知識點列表
>211．某 Python 程序如下：
import random
a=[58，69，78，80，83，84，90，90，95]
key=random.randint（35，45）*2
i=0；j=len（a）-1；s=（ ）
while i＜=j：
m=（i+j）//2
if key==a[m]：
break
elif key＜a[m]：
j=m-1
else：
i=m+1
s.append（a[m]）
則執行該程序段后，數組s中的元素不可能為（ ）發布：2024/5/23 20:38:36組卷：0引用：1難度：0.4212．某二分查找算法的Python程序段如下：
d=[11，19，25，33，47，58]
i,j=0，5
f=False
key=int（input（ ））
while i＜=j and f==False：
m=（i+j）//2
if key==d[m]：
f=True
if key＜d[m]：
j=m-1
else：
i=m+1
運行該程序后輸入key值為“33”，運行程序結束后下列說法不正確的是（ ）發布：2024/5/23 20:38:36組卷：2引用：1難度：0.7213．有一個含7個節點的單向鏈表，設有頭指針head和尾指針tail,下列操作需遍歷多個節點的是（ ）
發布：2024/5/23 20:38:36組卷：5引用：2難度：0.5214．下列代碼創建了一個擁有4個節點的雙鏈表a：
a=[[2，2，3]，[8，3，-1]，[0，-1，0]，[4，0，1]]
head=2
則其頭節點和尾節點數據域的值分別為（ ）發布：2024/5/23 20:38:36組卷：5引用：1難度：0.5215．一頭指針 head=2 的單向鏈表 L=[[30，4]，[10，-1]，[20，0]，[15，1]，[21，3]]通過以下 Python 程序段，轉換為原鏈表的逆序鏈表，即頭指針 head=1，L=[[30，2]，[10，3]，[20，-1]，[15，4]，[21，0]]。
上述程序段中方框處可選的語句為：
①p=tmp ②q=p ③L[p][1]=q
則方框處語句依次為（ ）發布：2024/5/23 20:38:36組卷：11引用：5難度：0.5216．文字、符號、音頻、圖像、視頻等都屬于（ ）
發布：2024/5/23 20:38:36組卷：22引用：6難度：0.5217．有如下Python程序段：
執行該程序段后，鏈表遍歷結果由初始狀態變為最終狀態，上述程序段中方框處可選代碼為：
①data[data[qt][1]][1]=pt
②data[qt][1]=data[pt][1]
③data[pt][1]=data[data[pt][1]][1]
則方框處代碼的正確順序是（ ）發布：2024/5/23 20:38:36組卷：7引用：3難度：0.5218．有一種 ASCII 字符加密的算法，其加密過程如下：
①將明碼中每個字符的 ASCII 碼轉為八位二進制，依次連接
②位置加密：每 4 位一組進行移位，第 1 組左移一位，并將原第一位數碼移至最后（如 0110 轉化為1100），第 2 組右移一位，并將原最后一位數碼移至頭部（如 0001 轉化為 1000），第 3 組左移...以此類推，實現位置加密，并將每組移動后的結果轉換成十進制，按順序連接
③值加密：隨機產生一個密鑰 key,在符號列表['+'，'*'，'//'，'%']中取出對應運算符號，將②中的十進制結果分別與密鑰 key 進行運算，順次連接求得該字符的密文，（如 key 為 3，取得運算符'%'，則字符'a'的高位密文為 12%3=0，低位密文為 8%3=2，順次連接后得'a'的密文為'02'
④將每個字符的密文順序連接，得到最終字符串密文。
用 Python 編寫的程序運行結果如下圖所示，請回答下列問題：
（1）當 key=3 時，輸入要加密的明文：“aA“則輸出的密文為。
（2）請在橫線處，填入適當的語句或語句表達式。
import random
def jzzh（x）：
s=''
for i in range（8）：
r=x%2
s=①
x=x//2
return s
def jisuan（x）：#進行 key 運算
m=0
if fh[key]=='+'：
m=x+key
elif fh[key]=='*'：
m=x*key
elif fh[key]=='//'：
m=x//key
elif fh[key]=='%'：
m=x%key
eturn m
def yidong（x）：
jg=''
n=len（x）//4
for i in range（n）：
if i%2==0：
f=②
else：
f=x[i*4+3]+x[i*4：i*4+3]
s=0
for j in f：#將 4 位二進制轉成十進制
s=s*2+int（j）
jg+=③
return jg
mingw=input（'請輸入要加密的明文：'）
fh=['+'，'*'，'//'，'%']
miw=''
global key
key=random.randint（0，3）
for a in mingw：
a=ord（a）
L=jzzh（a）
miw+=L
jieguo=yidong（miw）
print（“產生的隨機密鑰為：“，key,“\n 密文為：“，jieguo）發布：2024/5/23 20:38:36組卷：3引用：1難度：0.3219．某二分查找算法的Python程序段如下：
a=[8，17，24，30，36，40，55，58，61，66]
key=int（input（ ））
i,j=0，9
res=（ ）
while i＜=j：
m=（i+j+1）//2
if key==a[m]：
break
elif key＜a[m]：
j=m-1
else：
i=m+1
res.append（a[m]）
print（res）
執行該程序段，當輸入的值為30時，程序輸出結果為（ ）發布：2024/5/23 20:38:36組卷：4引用：1難度：0.5220．使用Nilakantha級數可用于計算Pi（π）的無窮級數，它的計算機結果比萊布尼茨公式更快地接近 Pi（π）的近似值。
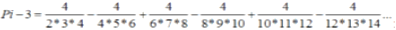
有下列代碼，通過前n項的計算，求Pi近似值：
s=0；n=0；i=0
n=int（input（“請輸入 n 的值：“））
for i in range（2，2*n+1，①______）：
s=s+②______
pi=3+s*4
print（pi）
劃線部分代碼正確的是（ ）發布：2024/5/23 20:38:36組卷：2引用：3難度：0.6
