2023-2024學年河南省鄭州一中高一(下)期中數學試卷
發布:2025/6/28 22:0:13
一、選擇題:本題共8小題,每小題5分,共40分.在每小題給出的四個選項中,只有一項是符合題目要求的。
-
1.已知△ABC的三邊上高的長度比分別為1:
:2,若△ABC的最短邊與最長邊的長度和為6,則△ABC面積為( )2A.2 2B. 7C. 6D.2 組卷:106引用:2難度:0.5 -
2.設i是虛數單位,若復數z(1+i)=i,則|z|=( )
A. 12B. 22C.1 D. 2組卷:104引用:5難度:0.8 -
3.已知z=3+4i,則
在復平面內對應的點位于( )1zA.第一象限 B.第二象限 C.第三象限 D.第四象限 組卷:27引用:2難度:0.8 -
4.已知α,β是不同的平面,m,n是不同的直線,則下列命題不正確的是( )
A.若m⊥α,m∥n,n?β,則α⊥β B.若m∥n,α∩β=m,則n∥α,n∥β C.若m∥n,m⊥α,則n⊥α D.若m⊥α,m⊥β,則α∥β 組卷:532引用:13難度:0.5 -
5.已知一個銅質的五棱柱的底面積為16cm2,高為4cm,現將它熔化后鑄成一個正方體的銅塊(不計損耗),那么鑄成的銅塊的棱長是( )
A.2cm B. 43cmC.4cm D.8cm 組卷:177引用:11難度:0.9 -
6.設
,e1是兩個不共線的向量,則向量e2=2a-e1,與向量e2=b+λe1,(λ∈R)共線,當且僅當λ的值為( )e2A.0 B.-1 C.-2 D.- 12組卷:50引用:3難度:0.8 -
7.已知兩條不同直線l,m,兩個不同平面α,β,則下列命題正確的是( )
A.若α∥β,l?α,m?β,則l∥m B.若α∥β,m∥α,l⊥β,則l⊥m C.若α⊥β,l⊥α,m⊥β,則l∥m D.若α⊥β,l∥α,m∥β,則l⊥m 組卷:590引用:10難度:0.6 -
8.
可以寫成①AC+AO;②OC-AO;③OC-OA;④OC-OC.其中正確的是( )OAA.①② B.②③ C.③④ D.①④ 組卷:543引用:4難度:0.9
二、選擇題:本題共3小題,每小題6分,共18分。每小題給出的選項有多項符合題目要求。全部選對的得6分,部分選對的得部分分,有選錯的得0分。
-
9.△ABC的內角A,B,C所對的邊分別為a,b,c,c=2,
,sinC+sin(B-A)-2sin2A=0,則下列命題正確的是( )C=π3A.b=2a B.△ABC的周長為 2+23C.△ABC的面積為 233D.△ABC的外接圓半徑為 433組卷:50引用:1難度:0.5 -
10.已知復數z滿足
,則( )z+2z=6+iA.z=2-i B. 是純虛數z1-2iC.|z|=5 D.復數z在復平面內對應的點在第四象限 組卷:83引用:4難度:0.8 -
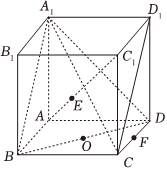 11.如圖,已知正方體ABCD-A1B1C1D1的棱長為1,O為底面ABCD的中心,AC1交平面A1BD于點E,點F為棱CD的中點,則( )
11.如圖,已知正方體ABCD-A1B1C1D1的棱長為1,O為底面ABCD的中心,AC1交平面A1BD于點E,點F為棱CD的中點,則( )A.A1,E,O三點共線 B.三棱錐A1-BCD的外接球的表面積為3π C.直線A1C與平面A1BD所成的角為45° D.過點A1,B,F的平面截該正方體所得截面的面積為 98組卷:140引用:6難度:0.4
三、填空題:本題共3小題,每小題5分,共15分。
-
12.在△ABC中,AC=2AB=4,∠BAC=60°.若點D在邊BC上,且滿足
,則AD=.BDDC=12組卷:42引用:2難度:0.5 -
13.已知向量
,則向量a=(3,4),b=(1,2)在向量a上的投影向量的坐標為 .b組卷:24引用:1難度:0.8 -
14.棱長為2的正方體ABCD-A1B1C1D1中,M,N分別為棱BB1,AB的中點,則三棱錐A1-D1MN的體積為 .
組卷:93引用:2難度:0.5
四、解答題:本題共5小題,共77分。解答應寫出文字說明、證明過程或演算步驟。
-
 15.如圖,在△ABC中,點P滿足,O是線段AP的中點,過點O的直線與邊AB,AC分別交于點E,F.PC=2BP
15.如圖,在△ABC中,點P滿足,O是線段AP的中點,過點O的直線與邊AB,AC分別交于點E,F.PC=2BP
(1)若,求AF=FC的值;AEEB
(2)若,EB=λAE(λ>0),求FC=μAF(μ>0)的最小值.1λ+1μ組卷:188引用:2難度:0.7 -
 16.如圖所示,A-BCP是圓錐的一部分,O是底面圓的圓心,,P是弧BC上一動點(不與B、C重合),滿足∠COP=θ,M是AB的中點,OA=2OB=2.∠BOC=2π3
16.如圖所示,A-BCP是圓錐的一部分,O是底面圓的圓心,,P是弧BC上一動點(不與B、C重合),滿足∠COP=θ,M是AB的中點,OA=2OB=2.∠BOC=2π3
(1)若MP∥平面AOC,求sinθ的值;
(2)若四棱錐M-OCPB的體積大于,求三棱錐A-MPC體積的取值范圍.14組卷:113引用:2難度:0.4 -
17.已知非零向量
的夾角為a,b.π6,|a|=23,a⊥(2a-b)
(1)求的值;a?b
(2)求.|a+b|組卷:23引用:2難度:0.7 -
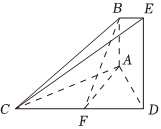 18.已知AB⊥平面ACD,DE⊥平面ACD,△ACD為等邊三角形,AD=DE=2,AB=1,F為CD的中點.
18.已知AB⊥平面ACD,DE⊥平面ACD,△ACD為等邊三角形,AD=DE=2,AB=1,F為CD的中點.
(1)求證:AF∥平面BCE;
(2)求證:平面BCE⊥平面CDE;
(3)求直線BF和平面BCE所成角的正弦值.組卷:215引用:3難度:0.5 -
19.(1)計算;
;(-1+i)(2+i)1+i
(2)在復數范圍內解關于x的方程:x2+4x+5=0.組卷:158引用:5難度:0.7


