當(dāng)前位置：試卷中心 > 試卷詳情

2023-2024學(xué)年廣東省深圳市龍崗區(qū)高二（上）期末數(shù)學(xué)試卷

發(fā)布：2025/6/28 23:0:12

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

1．已知正項等比數(shù)列{a_n}中，
2
a
5
+
a
6
-
1
a
4
+
a
5
=
3
，則a₆+a₇的最大值為（　　）
A．
2
3
B．
1
3
C．
3
2
D．
3
4
組卷：63引用：2難度：0.6
解析
2．曲線y=x²lnx在點（1，0）處的切線方程為（　　）
A．y=2x-1 B．y=2x-2 C．y=x-1 D．y=x+1
組卷：154引用：2難度：0.8
解析
3．已知數(shù)列{a_n}的前n項和為S_n，且滿足a₁=1，a_na_n+1=2S_n，設(shè)
b
n
=
a
n
3
n
，若存在正整數(shù)p,q（p＜q），使得b₁，b_p，b_q成等差數(shù)列，則（　　）
A．p=1 B．p=2 C．p=3 D．p=4
組卷：158引用：1難度：0.6
解析
4．已知函數(shù)f（x）=
x
e
x
和g（x）=
lnx
x
+b有相同的極大值，則b=（　　）
A．0 B．2 C．-1 D．-3
組卷：196引用：4難度：0.5
解析
5．雙曲線y²-3x²=9的漸近線方程是（　　）
A．y=±3x B．
y
=±
1
3
x
C．
y
=±
3
x
D．
y
=±
3
3
x
組卷：102引用：2難度：0.9
解析
6．已知直線l過A（-1，1）、B（1，3）兩點，則直線l的傾斜角的大小為（　　）
A．
π
4
B．
π
3
C．
2
π
3
D．
3
π
4
組卷：199引用：8難度：0.8
解析
7．已知拋物線y²=2px（p＞0）的焦點為F，準(zhǔn)線為l,過F的直線與拋物線交于點A、B，與直線l交于點D，若
AF
=
3
FB
，
|
BD
|
=
4
，則p=（　　）
A．1 B．3 C．2 D．4
組卷：212引用：8難度：0.6
解析
8．如圖，在棱長為1的正方體ABCD-A₁B₁C₁D₁中，點B到直線AC₁的距離為（　　）
A．
6
3
B．
6
6
C．
6
5
D．
2
6
3
組卷：570引用：6難度：0.9
解析

二、多項選擇題：本題共4小題，每小題5分，共20分。在每小題給出的選項中，有多項符合題目要求。全部選對的得5分，部分選對的得2分，有選錯的得0分。

9．在數(shù)列{a_n}中，其前n項和是S_n，則下列正確的是（　　）
A．
S
n
=
n
2
+
1
，則a_n=2n-1
B．若a₁=2，a_n+1=a_n+n+1，則
a
n
=
1
2
（
n
2
+
n
+
2
）
C．若a₁=2，na_n+1=（n+1）a_n，則a_n=2n
D．若
a
n
=
n
+
2
n
（
n
+
1
）
2
n
+
1
，則
S
4
=
79
160
組卷：51引用：4難度：0.5
解析
10．已知雙曲線C過點
（
2
2
，

1
）
且漸近線為
y
=±
1
2
x
，則下列結(jié)論正確的是（　　）
A．C的方程為
x
2
4
-
y
2
=
1
B．C的離心率為2
C．C的焦點到漸近線的距離為1
D．直線x-2y+1=0與C只有一個交點
組卷：30引用：3難度：0.7
解析
11．已知圓O：x²+y²=4，直線l與圓O交于P，Q兩點，A（2，2），若AP²+AQ²=40，則弦PQ的長度的取值可以是（　　）
A．2 B．
6
C．3 D．2
2
組卷：92引用：1難度：0.4
解析
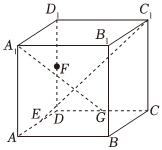12．如圖，棱長為2的正方體ABCD-A₁B₁C₁D₁中，點E，F(xiàn)，G分別是棱AD，DD₁，CD的中點，則（　　）
A．直線A₁G，C₁E為異面直線
B．二面角D₁-AC-B₁的余弦值為
1
3
C．直線A₁G與平面ADD₁A₁所成角的正切值為
2
4
D．過點B，E，F(xiàn)的平面截正方體的截面面積為9
組卷：247引用：4難度：0.3
解析

三、填空題：本題共4小題，每小題5分，共20分

13．在等差數(shù)列{a_n}中，a₄+a₅+a₆=90，則a₅=
．
組卷：71引用：1難度：0.8
解析
14．橢圓
x
2
a
2
+
y
2
5
=1（a為定值，且a＞
5
）的左焦點為F，直線x=m與橢圓交于點A，B，△FAB的周長的最大值是12，則該橢圓的離心率是
．
組卷：1551引用：18難度：0.5
解析
15．已知向量
a
=
（
2
，
1
，
3
）
，
b
=
（
1
，
1
，-
1
）
，
c
=
（
4
，
3
，
m
）
，若
a
，
b
，
c
共面，則m=
．
組卷：61引用：3難度：0.5
解析
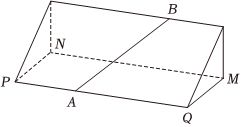
16．如圖，某人沿山坡PQB的直行道AB向上行走，直行道AB與坡腳（直）線PQ成60°角，山坡與地平面所成二面角B-PQ-M的大小為30°．若此人沿直行道AB向上行走了200米，那么此時離地平面的高度為
米．
組卷：53引用：2難度：0.6
解析

四、解答題：本題共6小題，共70分。解答應(yīng)寫出文字說明、證明過程或演算步驟。

17．記S_n為數(shù)列{a_n}的前n項和，已知a₂=3a₁．
（1）若數(shù)列{a_n}為等差數(shù)列，且a₁=1，求S_n；
（2）在（1）的條件下，若
b
n
=
S
n
?
2
a
n
n
，求數(shù)列{b_n}的前n項和T_n；
（3）在（1）的條件下，證明：當(dāng)n≥2時，
3
n
+
1
2
n
+
2
＜
1
S
1
+
1
S
2
+
?
+
1
S
n
＜
2
．
組卷：8引用：1難度：0.4
解析
18．在平面直角坐標(biāo)系xOy中，已知點P（2，4），圓O：x²+y²=4與x軸的正半軸的交點是Q，過點P的直線l與圓O交于不同的兩點A，B．
（1）設(shè)直線QA，QB的斜率分別是k₁，k₂，求k₁+k₂的值；
（2）設(shè)AB的中點為M，點
N
（
4
3
，
0
）
，若
MN
=
13
3
OM
，求△QAB的面積．
組卷：28引用：2難度：0.5
解析
19．已知函數(shù)f（x）=lnx-2x.
（1）求函數(shù)f（x）的極值；
（2）若
g
（
x
）
=
1
2
m
x
2
+
（
m
-
3
）
x
-
1
（
m
∈
R
）
，是否存在整數(shù)m使f（x）≤g（x）對任意x∈（0，+∞）成立？若存在，求出m的最小值；若不存在，請說明理由．
組卷：27引用：1難度：0.5
解析
20．已知函數(shù)f（x）=（lnx+ax+1）e^-x，其中常數(shù)a∈R．
（1）當(dāng)a≥0時，討論f（x）的單調(diào)性；
（2）當(dāng)
a
=
-
3
2
e
時，是否存在整數(shù)m使得關(guān)于x的不等式2m≥f（x）?x?e^x+3在區(qū)間（0，e）內(nèi)有解？若存在，求出整數(shù)m的最小值；若不存在，請說明理由．
參考數(shù)據(jù)：ln2≈0.69，e≈2.72，e²≈7.39，e^-2≈0.14
組卷：123引用：2難度：0.1
解析
21．已知橢圓 C：
x
2
a
2
+
y
2
b
2
=
1
（
a
?
b
＞
0
）
的上、下頂點分別為A，B，左頂點為D，△ABD是面積為
3
的正三角形．
（1）求橢圓C的方程；
（2）過橢圓外一點M（m,0）的直線交橢圓于P，Q兩點，已知點P與點P'關(guān)于x軸對稱，直線P'Q與x軸交于點K；若∠AKB是鈍角，求m的取值范圍．
組卷：92引用：3難度：0.3
解析
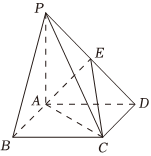22．如圖，在四棱錐P-ABCD中，底面ABCD為正方形，PA⊥平面ABCD，E為PD上的動點．
（1）確定E的位置，使 PB∥平面AEC并證明；
（2）設(shè)PA=AB=2，且在第（1）問的結(jié)論下，求二面角C-AE-D的正弦值．
組卷：38引用：1難度：0.5
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業(yè) 發(fā)布測評 反向細(xì)目表 平行組卷 下載答題卡 試卷分析 在線訓(xùn)練 收藏試卷

充值會員，資源免費下載

2023-2024學(xué)年廣東省深圳市龍崗區(qū)高二（上）期末數(shù)學(xué)試卷

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

1．已知正項等比數(shù)列{an}中，2a5+a6-1a4+a5=3，則a6+a7的最大值為（ ）

2．曲線y=x2lnx在點（1，0）處的切線方程為（ ）

3．已知數(shù)列{an}的前n項和為Sn，且滿足a1=1，anan+1=2Sn，設(shè)bn=an3n，若存在正整數(shù)p,q（p＜q），使得b1，bp，bq成等差數(shù)列，則（ ）

4．已知函數(shù)f（x）=xex和g（x）=lnxx+b有相同的極大值，則b=（ ）

5．雙曲線y2-3x2=9的漸近線方程是（ ）

6．已知直線l過A（-1，1）、B（1，3）兩點，則直線l的傾斜角的大小為（ ）

7．已知拋物線y2=2px（p＞0）的焦點為F，準(zhǔn)線為l,過F的直線與拋物線交于點A、B，與直線l交于點D，若AF=3FB，|BD|=4，則p=（ ）

8．如圖，在棱長為1的正方體ABCD-A1B1C1D1中，點B到直線AC1的距離為（ ）

二、多項選擇題：本題共4小題，每小題5分，共20分。在每小題給出的選項中，有多項符合題目要求。全部選對的得5分，部分選對的得2分，有選錯的得0分。

9．在數(shù)列{an}中，其前n項和是Sn，則下列正確的是（ ）

10．已知雙曲線C過點（22， 1）且漸近線為y=±12x，則下列結(jié)論正確的是（ ）

11．已知圓O：x2+y2=4，直線l與圓O交于P，Q兩點，A（2，2），若AP2+AQ2=40，則弦PQ的長度的取值可以是（ ）

12．如圖，棱長為2的正方體ABCD-A1B1C1D1中，點E，F(xiàn)，G分別是棱AD，DD1，CD的中點，則（ ）

三、填空題：本題共4小題，每小題5分，共20分

13．在等差數(shù)列{an}中，a4+a5+a6=90，則a5=．

14．橢圓x2a2+y25=1（a為定值，且a＞5）的左焦點為F，直線x=m與橢圓交于點A，B，△FAB的周長的最大值是12，則該橢圓的離心率是．

15．已知向量a=（2，1，3），b=（1，1，-1），c=（4，3，m），若a，b，c共面，則m=．

16．如圖，某人沿山坡PQB的直行道AB向上行走，直行道AB與坡腳（直）線PQ成60°角，山坡與地平面所成二面角B-PQ-M的大小為30°．若此人沿直行道AB向上行走了200米，那么此時離地平面的高度為 米．

四、解答題：本題共6小題，共70分。解答應(yīng)寫出文字說明、證明過程或演算步驟。

19．已知函數(shù)f（x）=lnx-2x.（1）求函數(shù)f（x）的極值；（2）若g（x）=12mx2+（m-3）x-1（m∈R），是否存在整數(shù)m使f（x）≤g（x）對任意x∈（0，+∞）成立？若存在，求出m的最小值；若不存在，請說明理由．

22．如圖，在四棱錐P-ABCD中，底面ABCD為正方形，PA⊥平面ABCD，E為PD上的動點．（1）確定E的位置，使 PB∥平面AEC并證明；（2）設(shè)PA=AB=2，且在第（1）問的結(jié)論下，求二面角C-AE-D的正弦值．

1．已知正項等比數(shù)列{a_n}中，
2
a
5
+
a
6
-
1
a
4
+
a
5
=
3
，則a₆+a₇的最大值為（　　）

2．曲線y=x²lnx在點（1，0）處的切線方程為（　　）

3．已知數(shù)列{a_n}的前n項和為S_n，且滿足a₁=1，a_na_n+1=2S_n，設(shè)
b
n
=
a
n
3
n
，若存在正整數(shù)p,q（p＜q），使得b₁，b_p，b_q成等差數(shù)列，則（　　）

4．已知函數(shù)f（x）=
x
e
x
和g（x）=
lnx
x
+b有相同的極大值，則b=（　　）

5．雙曲線y²-3x²=9的漸近線方程是（　　）

6．已知直線l過A（-1，1）、B（1，3）兩點，則直線l的傾斜角的大小為（　　）

7．已知拋物線y²=2px（p＞0）的焦點為F，準(zhǔn)線為l,過F的直線與拋物線交于點A、B，與直線l交于點D，若
AF
=
3
FB
，
|
BD
|
=
4
，則p=（　　）

8．如圖，在棱長為1的正方體ABCD-A₁B₁C₁D₁中，點B到直線AC₁的距離為（　　）

9．在數(shù)列{a_n}中，其前n項和是S_n，則下列正確的是（　　）

10．已知雙曲線C過點
（
2
2
，

1
）
且漸近線為
y
=±
1
2
x
，則下列結(jié)論正確的是（　　）

11．已知圓O：x²+y²=4，直線l與圓O交于P，Q兩點，A（2，2），若AP²+AQ²=40，則弦PQ的長度的取值可以是（　　）

12．如圖，棱長為2的正方體ABCD-A₁B₁C₁D₁中，點E，F(xiàn)，G分別是棱AD，DD₁，CD的中點，則（　　）

13．在等差數(shù)列{a_n}中，a₄+a₅+a₆=90，則a₅=
．

14．橢圓
x
2
a
2
+
y
2
5
=1（a為定值，且a＞
5
）的左焦點為F，直線x=m與橢圓交于點A，B，△FAB的周長的最大值是12，則該橢圓的離心率是
．

15．已知向量
a
=
（
2
，
1
，
3
）
，
b
=
（
1
，
1
，-
1
）
，
c
=
（
4
，
3
，
m
）
，若
a
，
b
，
c
共面，則m=
．

16．如圖，某人沿山坡PQB的直行道AB向上行走，直行道AB與坡腳（直）線PQ成60°角，山坡與地平面所成二面角B-PQ-M的大小為30°．若此人沿直行道AB向上行走了200米，那么此時離地平面的高度為
米．

22．如圖，在四棱錐P-ABCD中，底面ABCD為正方形，PA⊥平面ABCD，E為PD上的動點．
（1）確定E的位置，使 PB∥平面AEC并證明；
（2）設(shè)PA=AB=2，且在第（1）問的結(jié)論下，求二面角C-AE-D的正弦值．