2023-2024學(xué)年四川省宜賓市敘州二中高二（上）期中數(shù)學(xué)試卷

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的.

• 1．已知點(diǎn)A（-1，3），點(diǎn)B（

  3

  ，-

  3

  ），則直線AB的傾斜角為（　　）

  A．30°

  B．45°

  C．120°

  D．135°
  組卷：72引用：1難度：0.8

  解析

• 2．圓x²+y²-2x+6y+6=0的圓心和半徑分別為（　　）

  A．圓心（1，3），半徑為2	B．圓心（1，-3），半徑為2
  C．圓心（-1，3），半徑為4	D．圓心（1，-3），半徑為4
  組卷：172引用：6難度：0.7

  解析

• 3．過點(diǎn)（3，-6）且在兩坐標(biāo)軸上的截距相等的直線的方程是（　　）

  A．2x+y=0	B．x+y+3=0
  C．x-y+3=0	D．x+y+3=0或2x+y=0
  組卷：377引用：6難度：0.9

  解析

• 4．某社會(huì)調(diào)查機(jī)構(gòu)就某地居民的月收入情況調(diào)查了10000人，并根據(jù)所得數(shù)據(jù)畫了樣本的頻率分布直方圖（如圖）．為了分析居民的收入與年齡、學(xué)歷、職業(yè)等方面的關(guān)系，要從這10000人中再用分層抽樣方法抽出200人作進(jìn)一步調(diào)查，則在[2500，3000）（元）月收入段應(yīng)抽出人數(shù)是（　　）
  

  A．100

  B．50

  C．40

  D．25
  組卷：11引用：2難度：0.8

  解析

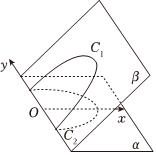• 5．如圖二面角α-y-β的大小為60°，平面β上的曲線C₁是橢圓的一部分，平面α上的曲線C₂是圓的一部分，平面β上的曲線C₁在平面α上的正投影為曲線C₂，曲線C₂在直角坐標(biāo)系xOy下的方程x²+y²=4（0≤x≤2），則曲線C₁的離心率為（　　）

  A． e = 1 3

  B． e = 5 3

  C． e = 3 2

  D． e = 1 2
  組卷：28引用：1難度：0.7

  解析

• 6．已知?jiǎng)又本€l：（m+3）x-（m+2）y+m=0與圓C：（x-3）²+（y-4）²=9則直線l被圓C所截得的弦長(zhǎng)的最小值是（　　）

  A． 10

  B． 6

  C． 2 7

  D． 2 2
  組卷：125引用：1難度：0.5

  解析

• 7．已知向量

  a

  =（1，2），

  c

  =（m,-1），若

  a

  ⊥（

  a

  -

  c

  ），則實(shí)數(shù)m的值為（　　）

  A．9

  B．7

  C．17

  D．21
  組卷：312引用：11難度：0.7

  解析
• 8．系統(tǒng)找不到該試題

二．選擇題：本題共4小題，每小題5分，共20分.在每小題給出的選項(xiàng)中，有多項(xiàng)符合題目要求.全部選對(duì)的得5分，部分選對(duì)的得2分，有選錯(cuò)的得0分.

• 9．下列說法正確的是（　　）

  A． a = （ 2 ，- 1 ） 是直線x+2y-3=0的一個(gè)方向向量

  B．點(diǎn)（0，2）關(guān)于直線y=x+1的對(duì)稱點(diǎn)為（1，1）

  C．過（x1，y1），（x2，y2）兩點(diǎn)的直線方程為 y - y 1 y 2 - y 1 = x - x 1 x 2 - x 1

  D．“ab=4”是“直線2x+ay-1=0與直線bx+2y-2=0平行”的充要條件
  組卷：55引用：1難度：0.8

  解析

• 10．下列函數(shù)中，在區(qū)間（0，+∞）單調(diào)遞減的是（　　）

  A． y = 1 x 2

  B．y=ln（x+1）

  C． y = x + 1 x

  D．y=2-x
  組卷：48引用：1難度：0.8

  解析

• 11．某展會(huì)安排了分別標(biāo)有序號(hào)為“1號(hào)”“2號(hào)”“3號(hào)”的三輛車，等可能的隨機(jī)順序前往酒店接嘉賓．某嘉賓突發(fā)奇想，設(shè)計(jì)了兩種乘車方案．方案一：不乘坐第一輛車，若第二輛車的車序號(hào)大于第一輛車的車序號(hào)，就乘坐此車，否則乘坐第三輛車；方案二：直接乘坐第一輛車．記方案一與方案二坐到“3號(hào)”車的概率分別為P₁，P₂，則（　　）

  A． P 1 ? P 2 = 1 6

  B． P 1 + P 2 = 1 2

  C． P 1 + P 2 = 5 6

  D．P1＞P2
  組卷：73引用：6難度：0.7

  解析

• 12．已知正方體ABCD-A₁B₁C₁D₁的棱長(zhǎng)為2，B₁D₁上有兩個(gè)動(dòng)點(diǎn)E，F(xiàn)，且EF=1，則下列結(jié)論中正確的是（　　）

  A．直線AE和直線CC1始終異面

  B．直線AC與平面BEF所成角為90°

  C．△AEF的面積與△BEF的面積相等

  D．三棱錐B-AEF的體積為定值
  組卷：142引用：1難度：0.5

  解析

三、填空題：本題共4小題，每小題5分，共20分．

• 13．把橢圓

  x

  2

  25

  +

  y

  2

  9

  =

  1

  繞左焦點(diǎn)按順時(shí)針方向旋轉(zhuǎn)90°，則所得橢圓的準(zhǔn)線方程為

  ．
  組卷：28引用：1難度：0.5

  解析

• 14．在△ABC中，∠ABC=45°，∠ACB=60°，△ABC繞BC旋轉(zhuǎn)一周，記以AB為母線的圓錐為M₁，記以AC為母線的圓錐為M₂，m是圓錐M₁任一母線，則圓錐M₂的母線中與m垂直的直線有

  條．
  組卷：313引用：1難度：0.5

  解析

• 15．已知直線l₁：ax-3y+1=0與直線l₂：2x+（a+1）y+1=0垂直，則a=

   

  ．
  組卷：54引用：2難度：0.7

  解析

• 16．在平面直角坐標(biāo)系xOy中，圓O：x²+y²=2被直線y=x+a截得的弦長(zhǎng)2，則實(shí)數(shù)a的值為

  ．
  組卷：335引用：7難度：0.8

  解析

四、解答題：本題共6小題，共70分．解答應(yīng)寫出文字說明、證明過程或演算步驟．

• 17．如圖所示正四棱錐S-ABCD，SA=SB=SC=SD=2，AB=

  2

  ，P為側(cè)棱SD上一動(dòng)點(diǎn)．（1）若直線SB∥面ACP，求證：P為棱SD的中點(diǎn)；
  （2）若SP=3PD，求：側(cè)棱SC上是否存在一點(diǎn)E，使得BE∥平面PAC．若存在，求

  SE

  EC

  的值；若不存在，試說明理由．
  組卷：186引用：2難度：0.5

  解析

• 18．已知圓C經(jīng)過兩點(diǎn)A（2，2），B（3，3），且圓心C在直線x-y+1=0上．
  （1）求圓C的標(biāo)準(zhǔn)方程；
  （2）設(shè)直線l：y=kx+1與圓C相交于M，N兩點(diǎn)，O為坐標(biāo)原點(diǎn)，若

  OM

  ?

  ON

  =

  64

  5

  ，求|MN|的值．
  組卷：182引用：3難度：0.6

  解析

• 19．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

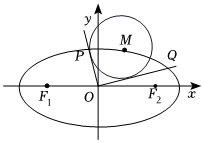  =1（a＞b＞0）的離心率為

  3

  2

  ，設(shè)M（x₀，y₀）是C上的動(dòng)點(diǎn)，以M為圓心作一個(gè)半徑r=2的圓，過原點(diǎn)作該圓的兩切線分別與橢圓C交于點(diǎn)P、Q，若存在圓M與兩坐標(biāo)軸都相切．
  （1）求橢圓C的方程；
  （2）若直線OP，OQ的斜率都存在且分別為k₁，k₂，求證：k₁k₂為定值；
  （3）求|OP|?|OQ|的最大值．
  組卷：31引用：1難度：0.5

  解析

• 20．（1）已知直線l₁：2x+y-1=0；l₂：mx+4y+n=0（m,n為常數(shù)）．若l₁⊥1₂，求m的值；
  （2）求焦點(diǎn)在坐標(biāo)軸上，長(zhǎng)軸長(zhǎng)為6，焦距為2的橢圓標(biāo)準(zhǔn)方程．
  組卷：121引用：1難度：0.8

  解析

• 21．如圖，矩形ABCD的兩條對(duì)角線相交于點(diǎn)M（2，0），AB邊所在直線的方程為x-3y-6=0，點(diǎn)T（-1，1）在AD邊所在直線上．
  （1）AD邊所在直線的方程；
  （2）矩形ABCD外接圓的方程．
  組卷：1929引用：46難度：0.3

  解析

• 22．第19屆亞運(yùn)會(huì)將于2023年9月23日在我國(guó)杭州舉行，這是繼北京亞運(yùn)會(huì)后，我國(guó)第二次舉辦這一亞洲最大的體育盛會(huì)，為迎接這一體育盛會(huì)，浙江某大學(xué)舉辦了一次主題為“喜迎杭州亞運(yùn)，講好浙江故事”的知識(shí)競(jìng)賽，并從所有參賽大學(xué)生中隨機(jī)抽取了40人，統(tǒng)計(jì)他們的競(jìng)賽成績(jī)，并將成績(jī)分成4組：[60，70），[70，80），[80，90），[90，100]（單位：分），得到如下的頻率分布直方圖．
  （1）現(xiàn)從該樣本中隨機(jī)抽取2人的成績(jī)，求這2人中至少有1人成績(jī)不低于90分的概率；
  （2）由頻率分布直方圖可以認(rèn)為，這次競(jìng)賽中所有參賽大學(xué)生的競(jìng)賽成績(jī)X近似服從正態(tài)分布N（μ，σ²），其中μ為樣本平均數(shù)（同一組數(shù)據(jù)用該組數(shù)據(jù)的區(qū)間中點(diǎn)值作代表），σ≈9.5，試用正態(tài)分布知識(shí)解決下列問題：
  ①若這次競(jìng)賽共有1.2萬名大學(xué)生參加，試估計(jì)競(jìng)賽成績(jī)超過90.5分的人數(shù)（結(jié)果精確到個(gè)位）；
  ②現(xiàn)從所有參賽的大學(xué)生中隨機(jī)抽取5人進(jìn)行座談，設(shè)其中競(jìng)賽成績(jī)超過81分的人數(shù)為Y，求隨機(jī)變量Y的期望．
  附：若隨機(jī)變量X服從正態(tài)分布N（μ，σ²），則P（μ-σ＜X≤μ+σ）≈0.6827，P（μ-2σ＜X≤μ+2σ）≈0.9544，P（μ-3σ＜X≤μ+3σ）≈0.9973．
  組卷：64引用：3難度：0.6

  解析