當前位置：試卷中心 > 試卷詳情

2022-2023學年湖南省湘西州高一（下）期末數學試卷

發布：2025/6/29 3:0:17

一、單項選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

1．設向量
a
，
b
滿足
|
a
|
=
2
，
|
b
|
=
1
，若?t∈R，
|
a
+
t
b
|
＜
|
a
+
b
|
，則向量
a
與
b
的夾角不等于（　　）
A．30° B．60° C．120° D．150°
組卷：287引用：3難度：0.7
解析
2．下列命題正確的是（　　）
A．單位向量都相等
B．模為0的向量與任意向量共線
C．平行向量不一定是共線向量
D．任一向量與它的相反向量不相等
組卷：704引用：7難度：0.9
解析
3．數據0，1，3，4，5，6，8，9的第60百分位數為（　　）
A．6 B．5.5 C．5 D．4
組卷：38引用：2難度：0.8
解析
4．已知二面角α-l-β，P∈α，點P與β的距離為m,到l的距離為2m,則二面α-l-β的度數為（　　）
A．90° B．60° C．45° D．30°
組卷：154引用：2難度：0.5
解析
5．關于直線l,m及平面α，β，下列命題正確的是（　　）
A．若l∥α，α∩β=m,則l∥m B．若l⊥α，m⊥β，l⊥m,則α⊥β
C．若l∥m,α⊥β，m⊥α，則l∥β D．若l∥α，m⊥l,則m⊥α
組卷：50引用：2難度：0.6
解析
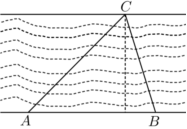6．如圖，為了測量河的寬度，在岸邊選定兩點A，B，望對岸的標記物C，測得∠CAB=45°，∠CBA=60°，AB=60米，則河的寬度為（　　）
A．30（3
2
+
6
）米 B．
30
（
3
-
3
）
米 C．
20
（
3
+
3
）
米 D．
30
（
3
-
1
）
米
組卷：54引用：1難度：0.6
解析
7．若a∈R，則“a=2”是復數“z=a²-4+（a+2）i”為純虛數的（　　）
A．充分不必要條件 B．必要不充分條件
C．充要條件 D．既不充分也不必要條件
組卷：112引用：9難度：0.8
解析
8．拋擲兩枚質地均勻的硬幣，設事件A₁=“第一枚硬幣正面朝上”，事件A₂=“第二枚硬幣反面朝上”，則下列結論中正確的為（　　）
A．A₁與A₂互為對立事件 B．A₁與A₂互斥
C．A₁與A₂相等 D．P（A₁）=P（A₂）
組卷：248引用：5難度：0.7
解析

二、多項選擇題：本題共4小題，每小題5分，共20分。在每小題給出的四個選項中，有多項符合題目要求。全部選對的得5分，部分選對的得2分，有選錯的得0分。

9．已知向量
a
=
（
2
，
1
）
，
b
=
（
cosθ
，
sinθ
）
，
（
0
≤
θ
≤
π
）
，下列命題正確的是（　　）
A．
若
a
⊥
b
，則
cosθ
=
-
3
3
B．
b
在
a
的投影向量的模為
1
2
，則向量
a
與
b
的夾角為
π
3
C．存在θ，使得
|
a
+
b
|
=
a
-
b
D．
a
?
b
的最大值為
3
組卷：8引用：1難度：0.6
解析
10．已知復數z=sinθ-icos2θ（0＜θ＜2π）的實部與虛部互為相反數，則θ的值可以為（　　）
A．
π
6
B．
π
2
C．
5
π
6
D．
3
π
2
組卷：24引用：3難度：0.8
解析

11．2021年5月31日，中共中央政治局召開會議，審議《關于優化生育政策促進人口長期均衡發展的決定》并指出，為進一步優化生育政策，積極應對人口老齡化，實施一對夫妻可以生育三個子女政策及配套支持措施．假定生男生女是等可能的，現隨機選擇一個有3個孩子的家庭，則（　　）

A．三個孩子都是男孩的概率為

B．這個家庭有女孩的概率為

C．第一孩是男孩的條件下，第二三孩也是男孩的概率為

D．這個家庭有女孩的條件下，該家庭也有男孩的概率為

組卷：31引用：1難度：0.7

解析

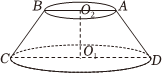12．某班級到一工廠參加社會實踐勞動，加工出如圖所示的圓臺O₁O₂，在軸截面ABCD中，AB=AD=BC=2cm,且CD=2AB，下列說法正確的是（　　）
A．該圓臺軸截ABCD面面積為
3
3
c
m
2
B．該圓臺的體積為
7
3
π
3
c
m
3
C．該圓臺的表面積為10πcm²
D．沿著該圓臺表面，從點C到AD中點的最短距離為5cm
組卷：101引用：3難度：0.6
解析

三、填空題：本題共4小題，每小題5分，共20分。

13．方程sinx=cos2x在區間[0，π]上的解集為
．
組卷：53引用：1難度：0.7
解析
14．青少年近視問題已經成為我國面臨的重要社會問題．現用分層隨機抽樣的方法調查某校學生的視力情況，該校三個年級的學生人數如表：

年級高一高二高三

人數 550 500 450

已知在抽取的樣本中，高二年級有20人，那么該樣本中高三年級的人數為
．
組卷：10引用：2難度：0.7
解析
15．復數z=（1+2i）（3-i），其中i為虛數單位，則z的實部是

．
組卷：1205引用：20難度：0.9
解析
16．已知圓錐的高為4，底面積為9π，則圓錐的表面積為
．
組卷：87引用：2難度：0.6
解析

四、解答題：本題共6小題，共70分，解答應寫出文字說明、證明過程或演算步驟.

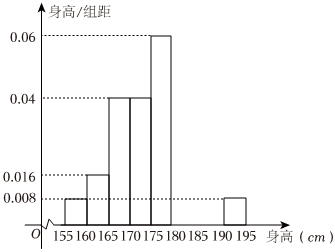17．從某學校的800名男生中隨機抽取50名測量身高，被測學生身高全部介于155cm和195cm之間，將測量結果按如下方式分成八組：第一組[155，160），第二組[160，165），…，第八組[190，195]，如圖是按上述分組方法得到的頻率分布直方圖的一部分，已知第一組與第八組人數相同，第六組的人數為4人．
（1）求第七組的頻率；
（2）估計該校的800名男生身高的80%分位數；（保留小數點后一位有效數字）
（3）若從身高屬于第六組和第八組的所有男生中隨機抽取兩名男生，記他們的身高分別為x,y,事件E={|x-y|≤5}，求樣本空間Ω及事件E的概率P（E）．
組卷：178引用：4難度：0.6
解析

18．體育強則中國強．站在“兩個一百年”奮斗目標交匯的歷史節點上，作為教育部直屬重點大學附中，西南大學附中始終高度重視學校體育工作，構建德智體美勞全面培養的教育體系．現從該校隨機抽取100名學生調查其運動習慣（稱每周運動不少于3次的為運動達標，否則為運動不達標），得到如表數據：

運動達標運動不達標合計

男 25 ___ 40

女 _ 40 _

合計 _ _ ___

（1）補全2×2列聯表，根據小概率值α=0.005的獨立性檢驗，能否認為運動達標與性別有關聯？
（2）用樣本估計總體，將頻率視為概率，現從該校所有男生中隨機抽取1名男生進行調查，從該校所有女生中隨機抽取2名女生進行調查，抽取的學生運動是否達標相互獨立，設隨機變量X表示這三人中運動達標的人數，求X的分布列與數學期望．
附：
χ
2
=
n
（
ad
-
bc
）
2
（
a
+
b
）
（
c
+
d
）
（
a
+
c
）
（
b
+
d
）

α 0.100 0.050 0.010 0.005 0.001

χ_α 2.706 3.841 6.635 7.879 10.828

組卷：34引用：2難度：0.5

解析

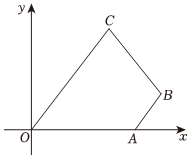19．如圖，已知O為平面直角坐標系的原點，A（4，0），點B，C在第一象限，且滿足
OC
=
3
AB
，
OA
?
AB
=
AB
?
BC
=
4
．
（1）求B和C的坐標；
（2）若AC交OB于點D，求cos∠ODA．
組卷：156引用：1難度：0.5
解析
20．在①bsin
A
+
B
2
=csinB，②
3
（
ccos
A
-
b
）
=
-
asin
C
，③
c
cos
C
=
a
+
b
cos
A
+
cos
B
這三個條件中任選一個，補充在下面的問題中，并解答．
在銳角△ABC中，內角A，B，C的對邊分別為a,b,c,且滿足_____．
（1）求角C的大小；
（2）若c=
3
，角A與角B的內角平分線相交于點D，求△ABD面積的取值范圍．
注：如果選擇多個條件分別解答，按第一個解答計分．
組卷：103引用：1難度：0.6
解析
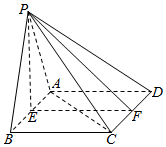21．四棱錐P-ABCD，底面為正方形ABCD，邊長為4，E為AB中點，PE⊥平面ABCD．
（1）若△PAB為等邊三角形，求四棱錐P-ABCD的體積；
（2）若CD的中點為F，PF與平面ABCD所成角為45°，求PC與AD所成角的大小．
組卷：3080引用：3難度：0.7
解析
22．定義在R上的非常值函數y=f（x）、y=g（x），若對任意實數x、y,均有f（x+y）?f（x-y）=g²（y）-g²（x），則稱y=g（x）為y=f（x）的相關函數．
（1）判斷g（x）=x+1是否為f（x）=x的相關函數，并說明理由；
（2）若y=g（x）為y=f（x）的相關函數，證明：y=f（x）為奇函數；
（3）在（2）的條件下，如果g（0）=1，g（3）=-1，當0＜x＜3時，-1＜g（x）＜1，且f（x+T）=f（x）對所有實數x均成立，求滿足要求的最小正數T，并說明理由．
組卷：34引用：2難度：0.5
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．若l∥α，α∩β=m,則l∥m	B．若l⊥α，m⊥β，l⊥m,則α⊥β
C．若l∥m,α⊥β，m⊥α，則l∥β	D．若l∥α，m⊥l,則m⊥α

A．充分不必要條件	B．必要不充分條件
C．充要條件	D．既不充分也不必要條件

A．A₁與A₂互為對立事件	B．A₁與A₂互斥
C．A₁與A₂相等	D．P（A₁）=P（A₂）

	運動達標	運動不達標	合計
男	25	_____	40
女	_____	40	_____
合計	_____	_____	_____

年級	高一	高二	高三
人數	550	500	450

2022-2023學年湖南省湘西州高一（下）期末數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

1．設向量a，b滿足|a|=2，|b|=1，若?t∈R，|a+tb|＜|a+b|，則向量a與b的夾角不等于（ ）

2．下列命題正確的是（ ）

3．數據0，1，3，4，5，6，8，9的第60百分位數為（ ）

4．已知二面角α-l-β，P∈α，點P與β的距離為m,到l的距離為2m,則二面α-l-β的度數為（ ）

5．關于直線l,m及平面α，β，下列命題正確的是（ ）

6．如圖，為了測量河的寬度，在岸邊選定兩點A，B，望對岸的標記物C，測得∠CAB=45°，∠CBA=60°，AB=60米，則河的寬度為（ ）

7．若a∈R，則“a=2”是復數“z=a2-4+（a+2）i”為純虛數的（ ）

8．拋擲兩枚質地均勻的硬幣，設事件A1=“第一枚硬幣正面朝上”，事件A2=“第二枚硬幣反面朝上”，則下列結論中正確的為（ ）

二、多項選擇題：本題共4小題，每小題5分，共20分。在每小題給出的四個選項中，有多項符合題目要求。全部選對的得5分，部分選對的得2分，有選錯的得0分。

9．已知向量a=（2，1），b=（cosθ，sinθ），（0≤θ≤π），下列命題正確的是（ ）

10．已知復數z=sinθ-icos2θ（0＜θ＜2π）的實部與虛部互為相反數，則θ的值可以為（ ）

12．某班級到一工廠參加社會實踐勞動，加工出如圖所示的圓臺O1O2，在軸截面ABCD中，AB=AD=BC=2cm,且CD=2AB，下列說法正確的是（ ）

三、填空題：本題共4小題，每小題5分，共20分。

13．方程sinx=cos2x在區間[0，π]上的解集為 ．

15．復數z=（1+2i）（3-i），其中i為虛數單位，則z的實部是 ．

16．已知圓錐的高為4，底面積為9π，則圓錐的表面積為 ．

四、解答題：本題共6小題，共70分，解答應寫出文字說明、證明過程或演算步驟.

19．如圖，已知O為平面直角坐標系的原點，A（4，0），點B，C在第一象限，且滿足OC=3AB，OA?AB=AB?BC=4．（1）求B和C的坐標；（2）若AC交OB于點D，求cos∠ODA．

21．四棱錐P-ABCD，底面為正方形ABCD，邊長為4，E為AB中點，PE⊥平面ABCD．（1）若△PAB為等邊三角形，求四棱錐P-ABCD的體積；（2）若CD的中點為F，PF與平面ABCD所成角為45°，求PC與AD所成角的大小．

1．設向量
a
，
b
滿足
|
a
|
=
2
，
|
b
|
=
1
，若?t∈R，
|
a
+
t
b
|
＜
|
a
+
b
|
，則向量
a
與
b
的夾角不等于（　　）

2．下列命題正確的是（　　）

3．數據0，1，3，4，5，6，8，9的第60百分位數為（　　）

4．已知二面角α-l-β，P∈α，點P與β的距離為m,到l的距離為2m,則二面α-l-β的度數為（　　）

5．關于直線l,m及平面α，β，下列命題正確的是（　　）

6．如圖，為了測量河的寬度，在岸邊選定兩點A，B，望對岸的標記物C，測得∠CAB=45°，∠CBA=60°，AB=60米，則河的寬度為（　　）

7．若a∈R，則“a=2”是復數“z=a²-4+（a+2）i”為純虛數的（　　）

8．拋擲兩枚質地均勻的硬幣，設事件A₁=“第一枚硬幣正面朝上”，事件A₂=“第二枚硬幣反面朝上”，則下列結論中正確的為（　　）

9．已知向量
a
=
（
2
，
1
）
，
b
=
（
cosθ
，
sinθ
）
，
（
0
≤
θ
≤
π
）
，下列命題正確的是（　　）

10．已知復數z=sinθ-icos2θ（0＜θ＜2π）的實部與虛部互為相反數，則θ的值可以為（　　）

12．某班級到一工廠參加社會實踐勞動，加工出如圖所示的圓臺O₁O₂，在軸截面ABCD中，AB=AD=BC=2cm,且CD=2AB，下列說法正確的是（　　）

13．方程sinx=cos2x在區間[0，π]上的解集為
．

15．復數z=（1+2i）（3-i），其中i為虛數單位，則z的實部是

．

16．已知圓錐的高為4，底面積為9π，則圓錐的表面積為
．

19．如圖，已知O為平面直角坐標系的原點，A（4，0），點B，C在第一象限，且滿足
OC
=
3
AB
，
OA
?
AB
=
AB
?
BC
=
4
．
（1）求B和C的坐標；
（2）若AC交OB于點D，求cos∠ODA．

21．四棱錐P-ABCD，底面為正方形ABCD，邊長為4，E為AB中點，PE⊥平面ABCD．
（1）若△PAB為等邊三角形，求四棱錐P-ABCD的體積；
（2）若CD的中點為F，PF與平面ABCD所成角為45°，求PC與AD所成角的大小．