2021-2022學年廣西河池市八校高二（上）第一次聯考數學試卷（文科）

一、選擇題：本大題共12小題，每小題5分.共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．無論實數t取何值，直線tx+y+t-1=0與圓（x-2）²+（y-2）²=m²恒有公共點，則實數m的取值范圍是（　　）

  A． m ＞ 10	B． m ≥ 10
  C． m ＜ - 10 或 m ＞ 10	D． m ≤ - 10 或 m ≥ 10
  組卷：42引用：1難度：0.7

  解析

• 2．已知各項均為正數的等比數列{a_n}滿足

  a

  1

  a

  3

  =

  1

  4

  ，a₂a₄=1，則a₆=（　　）

  A．2

  B．4

  C．8

  D．16
  組卷：248引用：2難度：0.7

  解析

• 3．數列{a_n}中，“a_n²=a_n-1?a_n+1（n≥2）”是“數列{a_n}為等比數列”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：210引用：5難度：0.6

  解析

• 4．函數f（x）=ln（2-x）的定義域是（　　）

  A．（2，+∞）

  B．[2，+∞）

  C．（-∞，2）

  D．（-∞，2]
  組卷：188引用：3難度：0.7

  解析

• 5．A為三角形ABC的一個內角．若sinA+cosA=

  12

  25

  ，2sinBcosC=sinA，則這個三角形的形狀不可能為（　　）

  A．銳角三角形	B．鈍角三角形
  C．等腰且鈍角三角形	D．等腰三角形
  組卷：17引用：0難度：0.9

  解析

• 6．已知空間兩不同直線m,n,兩不同平面α，β，下列命題正確的是（　　）

  A．若m∥α且n∥α，則m∥n

  B．若m⊥β且m∥n,則n∥β

  C．若m⊥α且m∥β，則α⊥β

  D．若m不垂直于α，且n?α，則m不垂直于n
  組卷：206引用：5難度：0.6

  解析

• 7．已知在10件產品中可能存在次品，從中抽取2件檢查，記次品數為X，已知

  P

  （

  X

  =

  1

  ）

  =

  16

  45

  ，且該產品的次品率不超過30%，則這10件產品中次品數n為（　　）

  A．1件

  B．2件

  C．8件

  D．2件或8件
  組卷：117引用：2難度：0.7

  解析

• 8．在△ABC中，角A、B、C的對邊分別為a、b、c,已知

  a

  =

  2

  ，

  b

  =

  3

  ，B=60°，那么角A等于（　　）

  A．135°

  B．90°

  C．45°

  D．30°
  組卷：83引用：16難度：0.9

  解析

• 9．在等差數列{a_n}中，已知S₆=10，S₁₂=30，則S₁₈=（　　）

  A．90

  B．40

  C．50

  D．60
  組卷：738引用：6難度：0.8

  解析

• 10．已知向量

  m

  =

  （

  1

  ，

  2

  ，

  3

  ）

  與

  n

  =

  （

  2

  ，

  x

  ,

  6

  ）

  垂直，則實數x的值為（　　）

  A．-10

  B．-4

  C．4

  D．10
  組卷：14引用：1難度：0.7

  解析

• 11．把函數y=sin3x的圖象向左平移

  π

  6

  ，可以得到的函數為（　　）

  A． y = sin （ 3 x + π 6 ）	B． y = sin （ 3 x - π 6 ）
  C．y=cos3x	D．y=cos（3x+ π 6 ）
  組卷：65引用：4難度：0.7

  解析
• 12．系統找不到該試題

二、填空題（本題共4小題，每小題5分，共20分）

• 13．在△ABC中，a²=b²+c²+bc,則A=

   

  ．
  組卷：207引用：30難度：0.7

  解析

• 14．在△ABC中，a²=b²+c²+bc,則A=

   

  ．
  組卷：30引用：6難度：0.8

  解析

• 15．△ABC的內角A，B，C所對的邊分別為a,b,c,若b=3，c=2，△ABC的面積為2sinB，cosA=

  ．
  組卷：40引用：1難度：0.6

  解析

• 16．數列{a_n}的通項公式為a_n=（-1）^n-1（4n-3），則它的前100項和S₁₀₀=

  ．
  組卷：249引用：8難度：0.7

  解析

三、解答題（共70分.解答應寫出文字說明、證明過程或演算步驟.）

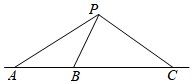• 17．如圖，在一條海防警戒線上的點A、B、C處各有一個水聲監測點，B、C兩點到A的距離分別為20千米和50千米，某時刻，B收到發自靜止目標P的一個聲波信號，8秒后A、C同時接收到該聲波信號，已知聲波在水中的傳播速度是1.5千米/秒．
  （1）設A到P的距離為x千米，用x表示B、C到P的距離，并求x的值；
  （2）求P到海防警戒線AC的距離．
  組卷：25引用：3難度：0.5

  解析

• 18．已知條件：①2a=b+2ccosB；②

  2

  asin

  A

  cos

  B

  +

  bsin

  2

  A

  =

  2

  3

  acos

  C

  ；③

  3

  sin

  C

  =

  3

  -

  2

  co

  s

  2

  C

  2

  ．
  從三個條件中任選一個，補充在下面的問題中，并解答．
  問題：在△ABC中，角A，B，C所對的邊分別為a,b,c,滿足：____．
  （1）求角C的大小；
  （2）若

  c

  =

  2

  3

  ，∠ABC與∠BAC的平分線交于點I，求△ABI周長的最大值．
  組卷：390引用：5難度：0.5

  解析

• 19．已知函數f（x）=|x-2a|-alnx,常數a∈R．
  （Ⅰ）求f（x）的單調區間；
  （Ⅱ）若函數f（x）有兩個零點x₁、x₂，且x₁＜x₂．
  （1）指出a的取值范圍，并說明理由；
  （2）求證：x₁?x₂＜8a³．
  組卷：85引用：3難度：0.5

  解析

• 20．已知項數大于3的數列{a_n}的各項和為S_n，且任意連續三項均能構成不同的等腰三角形的三邊長．
  （1）若a_n∈{1，2}（n=1，2，3，?，M），求M和S_n；
  （2）若a_n∈N₊（n=1，2，3，?，M），且M=8，求S_n的最小值．
  組卷：35引用：1難度：0.6

  解析

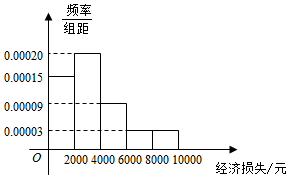• 21．2016年10月21日，臺風“海馬”導致江蘇、福建、廣東3省11市51個縣（市、區）189.9萬人受災，某調查小組調查了受災某小區的100戶居民由于臺風造成的經濟損失，將收集的數據分成[0，2000]，（2000，4000]，（4000，6000]，（6000，8000]，（8000，10000]五組，并作出頻率分布直方圖．
  （Ⅰ）臺風后居委會號召小區居民為臺風重災區捐款，小張調查的100戶居民捐款情況如表所示，在表格空白處填寫正確數字，并說明能否在犯錯誤的概率不超過0.05的前提下認為捐款數額超過或不超過500元和自身經濟損失是否超過4000元有關？
  （Ⅱ）將上述調查所得到的頻率視為概率，現在從該地區大量受災居民中，采用隨機抽樣的方法每次抽取1戶居民，抽取3次，記被抽取的3戶居民中自身經濟損失超過4000元的人數為ξ，若每次抽取的結果是相互獨立的，求ξ的分布列，期望E（ξ）和方差D（ξ）．
  

  	經濟損失不超過4000元	經濟損失超過4000元	總計
  捐款超過500元	60
  捐款不超過500元		10
  總計

  附：

  K

  2

  =

  n

  （

  ad

  -

  bc

  ）

  2

  （

  a

  +

  b

  ）

  （

  c

  +

  d

  ）

  （

  a

  +

  c

  ）

  （

  b

  +

  d

  ）

  ，其中n=a+b+c+d
  

  P（K2≥k0）	0.050	0.010	0.001
  k0	3.841	6.635	10.828
  組卷：36引用：1難度：0.3

  解析

• 22．設n∈N^*，有三個條件：①a_n是2與S_n的等差中項；②a₁=2，S_n+1=a₁（S_n+1）；③

  S

  n

  =

  2

  n

  +

  1

  -

  2

  ．在這三個條件中任選一個，補充在下列問題的橫線上，再作答．（如果選擇多個條件分別作答，那么按第一個解答計分）
  若數列{a_n}的前n項和為S_n，且 ______．
  （Ⅰ）求數列{a_n}的通項公式；
  （Ⅱ）若{a_n?b_n}是以2為首項，4為公差的等差數列，求數列{b_n}的前n項和T_n．
  組卷：221引用：5難度：0.4

  解析