人教B版（2019）必修第二冊《5.3.3 古典概型》2020年同步練習卷（1）
發布：2025/6/29 5:0:12
一、單選題
-
1．我國古代“伏羲八卦圖”中的八卦與二進制、十進制的互化關系如表，依據表中規律，A，B處應分別填寫（ ）
八卦 ? ? ? ? … ? … 二進制 000 001 010 011 … A … 十進制 0 1 2 3 … B … 組卷：165引用：4難度：0.8 -
2．拋擲一枚質地均勻的骰子（骰子的六個面上分別標有1，2，3，4，5，6個點）一次，觀察擲出向上的點數，設事件A為擲出向上為小于5的偶數點，事件B為擲出向上為3點，則P（A∪B）=（ ）
組卷：67引用：4難度：0.9 -
3．2022年北京冬奧會首先開賽的是冰壺競賽項目，冰壺（Curling）又稱擲冰壺，冰上溜石，是以隊為單位在冰上進行的一種投擲性競賽項目，被大家喻為冰上的“國際象棋”，它考驗參與者的體能與腦力，展現動靜之美，取舍之智慧．參賽選手只需要將冰壺擲到距離大本營中心最近的圓內就得分，大本營由4個同心圓組成，最大的圓外沿距離圓心為1.829米，第二個半徑為1.219米，第三個半徑為0.610米，最小的半徑為0.1534米，假設某選手等可能地將冰壺投進大本營區域中的任何位置，則他投擲冰壺進入最小圓形區域（以冰壺圓心是否位于圓內作為判斷標準）的概率約為（ ）
組卷：23引用：1難度：0.6 -
4．有甲、乙兩個袋子，甲袋子中有3個白球，2個黑球；乙袋子中有4個白球，4個黑球．現從甲袋子中任取2個球放入乙袋子，然后再從乙袋子中任取一個球，則此球為白球的概率為（ ）
組卷：329引用：7難度：0.7 -
5．“石頭、剪刀、布”，又稱“猜丁殼”，是一種流傳多年的猜拳游戲，起源于中國，然后傳到日本、朝鮮等地，隨著亞歐貿易的不斷發展，傳到了歐洲，到了近現代逐漸風靡世界．其游戲規則是：“石頭”勝“剪刀”、“剪刀”勝“布”、“布”勝“石頭”．若所出的拳相同，則為和局．小明和小華兩位同學進行三局兩勝制的“石頭、剪刀、布”游戲比賽，則比賽進行三次且小華獲勝的概率是（ ）
組卷：137引用：4難度：0.7
二、填空題
-
6．A，B，C三個地區爆發了流感，這三個地區分別有5%，4%，2%的人患了流感．假設這三個地區的人口比例為4：3：3．現從這三個地區中任意選取一個人，則這個人患流感的概率為 ．
組卷：9引用：2難度：0.7 -
7．按先后順序拋兩枚硬幣，觀察它們落地時正反面出現的情況，則恰好出現一個正面的概率是 ．
組卷：2引用：0難度：0.9 -
8．某次比賽中，9名評委對選手表現進行百分制打分，將選手的9個得分去掉一個最高分，去掉一個最低分，7個剩余分數的平均分為91．現場工作人員做了9個分數的莖葉圖，后來一個數據模糊，無法辨認，在圖中以x表示（見下圖），則x的值為 ．組卷：27引用：2難度：0.7
三、解答題
-
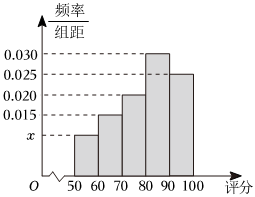9．為豐富學生的學習生活，某高中開設了“校本課程”．為了解學生對“校本課程”工作的認可程度，學校隨機調查了600名學生．根據這600名學生對“校本課程”工作認可程度給出的評分，分成[50，60），[60，70），[70，80），[80，90），[90，100]五組，得到如圖所示的頻率分布直方圖．
（1）求直方圖中x的值和第60百分位數；
（2）為了解部分學生給“校本課程”工作評分較低的原因，學校從評分低于80分的學生中用分層抽樣的方法隨機選取30人進行座談，求應選取評分在[60，70）的學生人數；
（3）若學生認可系數（認可系數=）低于0.85，“校本課程”工作按原方案繼續實施，否則需進一步整改．根據你所學的統計知識．結合認可系數，判斷“校本課程”工作是否需要進一步整改，并說明理由．認可程度平局分100組卷：70引用：3難度：0.7 -
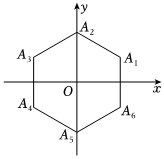10．周末來臨，小明以游戲方式決定是踢足球還是看電影，游戲規則如下：從A1，A2，A3，A4，A5，A6（如圖）這6個點中任取2個點．
（1）求取到點A1的概率；
（2）記選取的在y軸左側的點的個數為X．若X=0就踢足球，否則就看電影，求小明看電影的概率．組卷：4引用：1難度：0.7
四、選擇題
-
11．A，B，C，D四名學生的年齡關系如下．A，C的年齡之和與B，D的年齡之和相同，C，D的年齡之和大于A，B的年齡之和，B的年齡大于A，D的年齡之和，則A，B，C，D的年齡關系是（ ）
組卷：49引用：2難度：0.9 -
12．擲兩枚骰子，用隨機模擬方法估計出現點數之和為9的概率時，產生的整數值隨機數中，每幾個數字為一組 （ ）
組卷：18引用：1難度：0.8 -
13．某中學為提高學生的健康水平，增設了每天40分鐘的體育鍛煉課程，學生可以在跳繩、羽毛球、乒乓球、籃球、排球等課程中選擇一門．為了解該校學生參與乒乓球運動的情況，在全校班級中隨機抽取了7個班（將其編號為1，2，…，7），如表是這7個班參與乒乓球運動的人數統計表：
若從這7個班中隨機選取2個進行調查研究，則選出的2個班中至少有1個班參與乒乓球運動的人數超過12人的概率為（ ）班編號 1 2 3 4 5 6 7 人數/人 15 10 14 15 9 11 13 組卷：85引用：2難度：0.7 -
14．學校足球賽決賽計劃在周三、周四、周五三天中的某一天進行，如果這一天下雨則推遲至后一天，如果這三天都下雨則推遲至下一周，已知這三天下雨的概率均為
，則這周能進行決賽的概率為（ ）12組卷：106引用：3難度：0.7 -
15．5名射手獨立地進行射擊，設每人中靶的概率都是p,則5人都沒中靶的概率為（ ）
組卷：27引用：2難度：0.7 -
16．設20件產品中有5件不合格，從中任意取出2件，在所取得的產品中發現有一件不合格品，求另一件也是不合格品的概率為（ ）
組卷：10引用：1難度：0.7
五、填空題
-
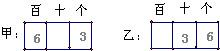17．如圖，三個方格代表三位數的數字，且甲、乙兩人分別將3、6的號碼排列如下，然后等機會在兩組1--9的9個號碼中各選出一個數，將它們分別在兩個空格中填上，則排出的數甲大于乙的概率是．組卷：6引用：2難度：0.5 -
18．拋擲甲、乙兩枚質地均勻的骰子，在甲骰子的點數為奇數的條件下，乙骰子的點數不小于甲骰子點數的概率為 ．
組卷：192引用：1難度：0.8
六、解答題
-
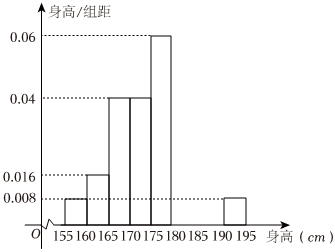19．從某學校的800名男生中隨機抽取50名測量身高，被測學生身高全部介于155cm和195cm之間，將測量結果按如下方式分成八組：第一組[155，160），第二組[160，165），…，第八組[190，195]，右圖是按上述分組方法得到的頻率分布直方圖的一部分，已知第一組與第八組人數相同，第六組的人數為4人．
（1）求第七組的頻率；
（2）估計該校的800名男生的身高的中位數；
（3）若從身高屬于第六組和第八組的所有男生中任取兩名男生，記他們的身高分別為x,y,事件E={|x-y|≤5}，求P（E）．組卷：159引用：18難度：0.7 -
20．第17屆亞運會于2014年9月19日至10月4日在韓國仁川進行，為了搞好接待工作，組委會招募了16名男志愿者和14名女志愿者，調查發現，男、女志愿者中分別有10人和6人喜愛運動，其余人不喜愛運動．
（1）根據以上數據完成以下2×2列聯表：
（2）根據列聯表的獨立性檢驗，能否在犯錯誤的概率不超過0.10的前提下認為性別與喜愛運動有關？喜愛運 動 不喜愛運動 總計 男 10 16 女 6 14 總計 30
（3）如果從喜歡運動的女志愿者中（其中恰有4人會外語），抽取2名負責翻譯工作，那么抽出的志愿者中至少有1人能勝任翻譯工作的概率是多少？參考公式：K2=，其中n=a+b+c+d.n（ad-bc）2（a+b）（c+d）（a+c）（b+d）
參考數據：P（K2≥k0） 0.40 0.25 0.10 0.010 k0 0.708 1.323 2.706 6.635 組卷：35引用：3難度：0.5