當前位置：試卷中心 > 試卷詳情

2021-2022學年江西省宜春市靖安中學高一（上）第一次月考數學試卷

發布：2025/6/29 5:0:12

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

1．已知函數f（x）=x²+x-1的定義域為R，f（x）可以表示為一個偶函數g（x）和一個奇函數h（x）之和，若不等式
g
（
kx
+
k
x
）
＜
g
（
x
2
+
1
x
2
+
1
）
對任意非零實數x恒成立，則實數k的取值范圍為（　　）
A．
（
-
3
2
，
3
2
）
B．
（
-
3
2
，
0
]
C．
（
-
∞
，-
3
2
）
∪
（
3
2
，
+
∞
）
D．
（
-
3
2
，
0
）
∪
（
0
，
3
2
）
組卷：72引用：3難度：0.5
解析
2．若關于x的不等式ax-b＞0的解集是（-1，+∞），則關于x的不等式ax²+bx＞0的解集為（　　）
A．（-∞，0）∪（1，+∞） B．（-∞，-1）∪（0，+∞）
C．（-1，0） D．（0，1）
組卷：37引用：2難度：0.8
解析
3．若正實數x,y滿足x+2y=4，不等式
m
2
+
1
3
m
＞
2
x
+
1
y
+
1
有解，則m的取值范圍是（　　）
A．
（
-
4
3
，
1
）
B．（-∞，-
4
3
）∪（1，+∞）
C．
（
-
1
，
4
3
）
D．（-∞，-1）∪（
4
3
，+∞）
組卷：157引用：8難度：0.5
解析
4．已知集合A={x|-2＜x≤1，x∈N}，則集合A中元素的子集個數為（　　）
A．1 B．2 C．3 D．4
組卷：123引用：5難度：0.8
解析
5．“x-1＞0”是“x²-1＞0”的（　　）
A．充分不必要條件 B．必要不充分條件
C．充分必要條件 D．既不充分也不必要條件
組卷：170引用：5難度：0.7
解析
6．若U={1，2，3，4}，M={1，2}，N={2，3}，則?_U（M∪N）是（　　）
A．{1，2，3} B．{2} C．{1，3，4} D．{4}
組卷：23引用：2難度：0.7
解析
7．若a＞0＞b,則（　　）
A．a³＞b³ B．|a|＞|b| C．
1
a
＜
1
b
D．ln（a-b）＞0
組卷：432引用：5難度：0.7
解析
8．已知函數f（x）=|x-1|，則與y=f（x）相等的函數是（　　）
A．g（x）=x-1 B．
h
（
x
）
=
x
-
1
，
x
＞
1
1
-
x
,
x
＜
1
C．
s
（
x
）
=
（
x
-
1
）
2
D．
t
（
x
）
=
（
x
-
1
）
2
組卷：155引用：3難度：0.9
解析

二、選擇題：本題共4小題，每小題5分，共20分。在每小題給出的選項中，有多項符合題目要求。全部選對的得5分，有選錯的得0分，部分選對的得3分。

9．若非空集合M，N，P滿足：M∩N=N，M∪P=P，則（　　）
A．P?M B．M∩P=M C．N∪P=P D．M∩?_PN=?
組卷：224引用：4難度：0.8
解析
10．下列等式能夠成立的為（　　）
A．
sin
15
°
cos
15
°=
1
2
B．sin75°cos15°+cos75°sin15°=1
C．cos105°cos75°-sin105°cos15°=-1
D．
3
sin
15
°
+
cos
15
°=
1
組卷：237引用：1難度：0.8
解析

11．下列結論正確的是（　　）

A．當x＞0時，

≥

B．若不等式ax²+bx+1＞0的解集為{x|-1＜x＜3}，則不等式3ax²+6bx+5＜0的解集為（-∞，-1）∪（5，+∞）

C．當

＜

時，

的最小值是5

D．對于?x∈R，ax²+4x≥2x²-1恒成立，則實數a的取值范圍是[6，+∞）

組卷：183引用：4難度：0.7

解析

12．已知不等式x²+2ax+b-1＞0的解集是{x|x≠d}，則b的值可能是（　　）
A．-1 B．3 C．2 D．0
組卷：66引用：3難度：0.8
解析

三、填空題：本大題共4個小題，每小題5分，共20分，把正確答案填在題中橫線上．

13．已知函數
f
（
x
）
=
a
x
-
1
，
x
＜
1
（
a
-
2
）
x
+
3
a
,
x
≥
1
滿足對任意x₁≠x₂，都有
f
（
x
1
）
-
f
（
x
2
）
x
1
-
x
2
＜
0
成立，則a的取值范圍是
．
組卷：22引用：1難度：0.6
解析
14．函數y=
lo
g
1
2
sinx
的定義域是
．
組卷：218引用：6難度：0.7
解析
15．若函數f（x）對于任意x有f′（x）=4x³，f（1）=-1，則此函數的解析式為
．
組卷：5引用：2難度：0.7
解析
16．若“?x∈R，使x²+（a+1）x+1＜0”為真命題，則實數a的取值范圍是
．
組卷：64引用：5難度：0.7
解析

四、解答題：本題共6小題，共70分．解答時應寫出文字說明、證明過程或演算步驟．

17．對于函數f（x），若f（x）=x,則稱x為f（x）的“不動點”，若f（f（x））=x,則稱x為f（x）的“穩定點”．函數f（x）的“不動點”和“穩定點”的集合分別記為A和B，即A={x|f（x）=x}，B={x|f（f（x））=x}
（1）證明：A?B；
（2）設f（x）=x²+ax+b,若A={-1，3}，求集合B．
組卷：101引用：2難度：0.9
解析
18．已知f（x）是二次函數，若f（0）=0，且f（x+1）=f（x）+x+1．
（1）求二次函數的解析式；
（2）當-1≤x≤1時，求二次函數的最大值與最小值．
組卷：21引用：2難度：0.7
解析
19．已知集合A={x|x²-3x+2≤0}，函數f（x）=x²-2ax+1．
（1）當a≠0時，解關于x的不等式f（x）≤3a²+1；
（2）若命題“存在x₀∈A，使得f（x₀）≤0”為假命題，求實數a的取值范圍．
組卷：1111引用：2難度：0.5
解析
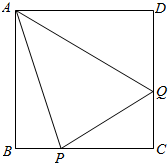20．如圖，某公司有一塊邊長為1百米的正方形空地ABCD，現要在正方形空地中規劃一個三角形區域PAQ種植花草，其中P，Q分別為邊BC，CD上的動點，∠PAQ=
π
4
，其它區域安裝健身器材，設∠BAP為θ弧度．
（1）求△PAQ面積S關于θ的函數解析式S（θ）；
（2）求面積S的最小值．
組卷：74引用：3難度：0.3
解析
21．已知U=R且A={x|x²-5x-6＜0}，B={x||x-2|≥1}，
求（1）A∩B；
（2）A∪B；
（3）（?_UA）∩（?_UB）．
組卷：51引用：5難度：0.5
解析
22．求下列方程的根：
（1）
x
-
5
+x=7；
（2）
（
x
2
x
+
2
）
2
-
2
x
2
x
+
2
-3=0．
組卷：9引用：1難度：0.7
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．（ - 3 2 ， 3 2 ）	B．（ - 3 2 ， 0 ]
C．（ - ∞ ，- 3 2 ） ∪ （ 3 2 ， + ∞ ）	D．（ - 3 2 ， 0 ） ∪ （ 0 ， 3 2 ）

A．（-∞，0）∪（1，+∞）	B．（-∞，-1）∪（0，+∞）
C．（-1，0）	D．（0，1）

A．（ - 4 3 ， 1 ）	B．（-∞，- 4 3 ）∪（1，+∞）
C．（ - 1 ， 4 3 ）	D．（-∞，-1）∪（ 4 3 ，+∞）

A．充分不必要條件	B．必要不充分條件
C．充分必要條件	D．既不充分也不必要條件

2021-2022學年江西省宜春市靖安中學高一（上）第一次月考數學試卷

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

1．已知函數f（x）=x2+x-1的定義域為R，f（x）可以表示為一個偶函數g（x）和一個奇函數h（x）之和，若不等式g（kx+kx）＜g（x2+1x2+1）對任意非零實數x恒成立，則實數k的取值范圍為（ ）

2．若關于x的不等式ax-b＞0的解集是（-1，+∞），則關于x的不等式ax2+bx＞0的解集為（ ）

3．若正實數x,y滿足x+2y=4，不等式m2+13m＞2x+1y+1有解，則m的取值范圍是（ ）

4．已知集合A={x|-2＜x≤1，x∈N}，則集合A中元素的子集個數為（ ）

5．“x-1＞0”是“x2-1＞0”的（ ）

6．若U={1，2，3，4}，M={1，2}，N={2，3}，則?U（M∪N）是（ ）

7．若a＞0＞b,則（ ）

8．已知函數f（x）=|x-1|，則與y=f（x）相等的函數是（ ）

二、選擇題：本題共4小題，每小題5分，共20分。在每小題給出的選項中，有多項符合題目要求。全部選對的得5分，有選錯的得0分，部分選對的得3分。

9．若非空集合M，N，P滿足：M∩N=N，M∪P=P，則（ ）

10．下列等式能夠成立的為（ ）

11．下列結論正確的是（ ）

12．已知不等式x2+2ax+b-1＞0的解集是{x|x≠d}，則b的值可能是（ ）

三、填空題：本大題共4個小題，每小題5分，共20分，把正確答案填在題中橫線上．

13．已知函數f（x）=ax-1，x＜1（a-2）x+3a,x≥1滿足對任意x1≠x2，都有f（x1）-f（x2）x1-x2＜0成立，則a的取值范圍是 ．

14．函數y=log12sinx的定義域是．

15．若函數f（x）對于任意x有f′（x）=4x3，f（1）=-1，則此函數的解析式為 ．

16．若“?x∈R，使x2+（a+1）x+1＜0”為真命題，則實數a的取值范圍是．

四、解答題：本題共6小題，共70分．解答時應寫出文字說明、證明過程或演算步驟．

18．已知f（x）是二次函數，若f（0）=0，且f（x+1）=f（x）+x+1．（1）求二次函數的解析式；（2）當-1≤x≤1時，求二次函數的最大值與最小值．

19．已知集合A={x|x2-3x+2≤0}，函數f（x）=x2-2ax+1．（1）當a≠0時，解關于x的不等式f（x）≤3a2+1；（2）若命題“存在x0∈A，使得f（x0）≤0”為假命題，求實數a的取值范圍．

21．已知U=R且A={x|x2-5x-6＜0}，B={x||x-2|≥1}，求（1）A∩B；（2）A∪B；（3）（?UA）∩（?UB）．

22．求下列方程的根：（1）x-5+x=7；（2）（x2x+2）2-2x2x+2-3=0．

1．已知函數f（x）=x²+x-1的定義域為R，f（x）可以表示為一個偶函數g（x）和一個奇函數h（x）之和，若不等式
g
（
kx
+
k
x
）
＜
g
（
x
2
+
1
x
2
+
1
）
對任意非零實數x恒成立，則實數k的取值范圍為（　　）

2．若關于x的不等式ax-b＞0的解集是（-1，+∞），則關于x的不等式ax²+bx＞0的解集為（　　）

3．若正實數x,y滿足x+2y=4，不等式
m
2
+
1
3
m
＞
2
x
+
1
y
+
1
有解，則m的取值范圍是（　　）

4．已知集合A={x|-2＜x≤1，x∈N}，則集合A中元素的子集個數為（　　）

5．“x-1＞0”是“x²-1＞0”的（　　）

6．若U={1，2，3，4}，M={1，2}，N={2，3}，則?_U（M∪N）是（　　）

7．若a＞0＞b,則（　　）

8．已知函數f（x）=|x-1|，則與y=f（x）相等的函數是（　　）

9．若非空集合M，N，P滿足：M∩N=N，M∪P=P，則（　　）

10．下列等式能夠成立的為（　　）

11．下列結論正確的是（　　）

12．已知不等式x²+2ax+b-1＞0的解集是{x|x≠d}，則b的值可能是（　　）

13．已知函數
f
（
x
）
=
a
x
-
1
，
x
＜
1
（
a
-
2
）
x
+
3
a
,
x
≥
1
滿足對任意x₁≠x₂，都有
f
（
x
1
）
-
f
（
x
2
）
x
1
-
x
2
＜
0
成立，則a的取值范圍是
．

14．函數y=
lo
g
1
2
sinx
的定義域是
．

15．若函數f（x）對于任意x有f′（x）=4x³，f（1）=-1，則此函數的解析式為
．

16．若“?x∈R，使x²+（a+1）x+1＜0”為真命題，則實數a的取值范圍是
．

18．已知f（x）是二次函數，若f（0）=0，且f（x+1）=f（x）+x+1．
（1）求二次函數的解析式；
（2）當-1≤x≤1時，求二次函數的最大值與最小值．

19．已知集合A={x|x²-3x+2≤0}，函數f（x）=x²-2ax+1．
（1）當a≠0時，解關于x的不等式f（x）≤3a²+1；
（2）若命題“存在x₀∈A，使得f（x₀）≤0”為假命題，求實數a的取值范圍．

21．已知U=R且A={x|x²-5x-6＜0}，B={x||x-2|≥1}，
求（1）A∩B；
（2）A∪B；
（3）（?_UA）∩（?_UB）．

22．求下列方程的根：
（1）
x
-
5
+x=7；
（2）
（
x
2
x
+
2
）
2
-
2
x
2
x
+
2
-3=0．