2023-2024學年湖南省長沙市明德中學高二(上)期末數學試卷
發布:2025/6/29 5:0:12
一、單選題(本題共8小題,每小題5分,共40分,在每小題給出的四個選項中,只有一項是符合題目要求的)
-
1.兩個等差數列{an}和{bn},其前n項和分別為Sn,Tn,且
,則SnTn=7n+2n+3等于( )a2+a20b7+b15A. 94B. 378C. 7914D. 14924組卷:1459引用:57難度:0.9 -
2.拋物線y=x2在點M(
,12)的切線的傾斜角是( )14A.30° B.45° C.60° D.90° 組卷:28引用:4難度:0.9 -
3.一個盒子里有3個分別標有號碼為1,2,3的小球,每次取出一個,記下它的標號后再放回盒子中,共取3次,則取得小球標號最大值是3的取法有( )
A.12種 B.15種 C.17種 D.19種 組卷:359引用:11難度:0.7 -
4.已知點P(4,a),若圓O:x2+y2=4上存在點A,使得線段PA的中點也在圓O上,則a的取值范圍是( )
A. [-33,33]B. [-25,25]C. (-∞,-33]∪[33,+∞)D. (-∞,-25]∪[25,+∞)組卷:143引用:5難度:0.5 -
5.若集合A={(x,y)|y=-x2},B={(x,y)|y=-x-2},則A∩B=( )
A.{(-1,-1),(2,-4)} B.{(-2,-4),(1,-1)} C.{2,-4} D.{2,-1} 組卷:28引用:2難度:0.7 -
6.已知
,則n=3∫20x2dx的展開式中含x2項的系數為( )(x+1x)nA.28 B.56 C.96 D.128 組卷:22引用:1難度:0.8 -
7.沈陽二中24屆籃球賽正如火如荼地進行中,全年級共20個班,每四個班一組,如1-4班為一組,5-8班為二組……進行單循環小組賽(沒有并列),勝出的5個班級和從余下隊伍中選出的數據最優秀的1個班級共6支球隊按抽簽的方式進行淘汰賽,最后勝出的三個班級再進行單循環賽,按積分的高低(假設沒有并列)決出最終的冠亞季軍,請問此次籃球賽學校共舉辦了多少場比賽?( )
A.51 B.42 C.39 D.36 組卷:21引用:2難度:0.7 -
8.系統找不到該試題
二、多選題(本題共4小題,每小題5分,共20分,在每小題給出選項中,有多項是符合題目要求的,全部選對得5分,部分選對得2分,有選錯的得0分)
-
9.已知數列{an}的前n項和為Sn,a1=1,Sn+1-1=Sn+2an,數列
的前n項和為Tn,n∈N*,則下列選項正確的為( ){2nan?an+1}A.數列{an+1-an}是等比數列 B.數列{an+1}是等差數列 C.數列{an}的通項公式為 an=2n-1D.Tn<1 組卷:52引用:2難度:0.5 -
 10.如圖,在四棱錐P-ABCD中,AB∥CD,AD=CD=1,∠BAD=120°,∠ACB=90°,PA⊥AC,平面PAC⊥平面PBC,點E在棱PC上且PE=3EC,點F是△PAD所在平面內的動點,點G是△PBC所在平面內的動點,且點G到直線BC的距離與到點E的距離相等,則( )
10.如圖,在四棱錐P-ABCD中,AB∥CD,AD=CD=1,∠BAD=120°,∠ACB=90°,PA⊥AC,平面PAC⊥平面PBC,點E在棱PC上且PE=3EC,點F是△PAD所在平面內的動點,點G是△PBC所在平面內的動點,且點G到直線BC的距離與到點E的距離相等,則( )A.PA⊥平面ABCD B.若二面角D-PC-A的余弦值為 ,則點A到平面PBC的距離為5555C.若 ,則動點F的軌跡長度為EF=104134πD.若PA=1,則AG的最小值為 32組卷:39引用:2難度:0.5 -
11.已知函數f(x)=Asin(2x+φ)(A>0,0<φ<π)的最大值為3,且f(x)的圖象關于直線
對稱,則下列說法正確的是( )x=π6A.函數f(x)的最小正周期為2π B. f(π3)=32C.函數f(x)的圖象關于點 對稱(-π12,0)D.函數f(x)在 上單調遞減[π6,π2]組卷:21引用:2難度:0.6 -
12.已知函數f(x)=
-4x+2,下列說法中正確的有( )13x3A.函數f(x)的極大值為 ,極小值為-223103B.當x∈[3,4]時,函數f(x)的最大值為 ,最小值為223-103C.函數f(x)的單調減區間為[-2,2] D.曲線y=f(x)在點(0,2)處的切線方程為y=-4x+2 組卷:261引用:13難度:0.7
三、填空題(本題共4小題,每小題5分,共20分)
-
13.奇函數f(x)=ax3+bx2+cx在x=1處有極值,則3a+b+c的值為.
組卷:125引用:8難度:0.9 -
14.復數
為虛數單位),則|z|=.z=|(3-i)i|+i2019(i組卷:0引用:1難度:0.8 -
15.
的展開式中常數項是 (用數字作答).(x+2x)6組卷:350引用:13難度:0.7 -
16.已知數列{an}滿足a1=1,an+1=2an,則該數列前8項之和S8=.
組卷:35引用:3難度:0.7
四.解答題(本題共6小題,共70分.解答題應寫出文字說明、證明過程或演算步驟)
-
17.已知函數f(x)=aln(x+1)-sinx.
(1)若f(x)在上單調遞減,求a的取值范圍;[π4,π2]
(2)證明:當a=1時,f(x)在上有且僅有一個零點.(π2,+∞)組卷:490引用:3難度:0.4 -
18.已知橢圓C:
的離心率為y2a2+x2b2=1(a>b>0),上焦點F到上頂點的距離為2.13
(1)求橢圓C的標準方程;
(2)過點F的直線l交橢圓C于P,Q兩點,與定直線l1:y=9交于點D,設,DP=λPF,證明:λ+μ為定值.DQ=μQF組卷:152引用:1難度:0.4 -
19.已知函數
.f(x)=cos2x+3sin(π-x)cos(π+x)-12
(1)求函數f(x)在上的值域[0,π2]
(2)在銳角△ABC中,內角A,B,C的對邊分別為a,b,c,已知f(A)=-1,a=2,bsinC=asinA,求△ABC的面積組卷:9引用:1難度:0.5 -
20.已知f(x)=x2-2x+alnx.
(1)若函數f(x)在x=2處取得極值,求實數a的值;
(2)若a=2,存在正實數x1,x2,使得f(x1)+f(x2)=x1+x2成立,求x1+x2的取值范圍.組卷:58引用:2難度:0.6 -
21.已知數列{an}的首項
,且滿足a1=45.an+1=4an3an+1(n∈N+)
(1)求證:數列為等比數列;{1an-1}
(2)若,數列{bn}前n項的和為Sn,求Sn.bn=(an1-an)(3n-1)組卷:223引用:5難度:0.4 -
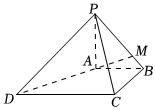 22.如圖,在四棱錐P-ABCD中,PA⊥平面ABCD,AB∥CD,AB⊥BC,PA=AB=BC=2,CD=4.
22.如圖,在四棱錐P-ABCD中,PA⊥平面ABCD,AB∥CD,AB⊥BC,PA=AB=BC=2,CD=4.
(1)證明:AD⊥PC;
(2)若M為線段PB的靠近B點的四等分點,判斷直線AM與平面PDC是否相交?如果相交,求出P到交點H的距離,如果不相交,說明理由.組卷:61引用:3難度:0.5


