當前位置：試卷中心 > 試卷詳情

2020-2021學年福建省寧德市部分達標中學高二（下）期中數學試卷

發布：2025/6/29 6:0:13

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

1．對于二項式
（
2
x
-
x
3
）
7
，四位同學作出了四種判斷：
①在展開式中沒有常數項；
②在展開式中存在常數項；
③在展開式中沒有x的一次項；
④在展開式中存在x的一次項
上述判斷中正確的是（　　）
A．①③ B．②③ C．②④ D．①④
組卷：23引用：1難度：0.8
解析
2．下列求導運算中，正確的是（　　）
A．（cosx）'=sinx B．（3^x）′=3^x
C．（xe^x）′=（x+1）e^x D．
（
lnx
x
）
′
=
1
-
lnx
x
組卷：232引用：3難度：0.7
解析
3．復數z=a²+a+（a²-a）i為純虛數，則實數a的值是（　　）
A．-1 B．1 C．0或-1 D．0或1
組卷：117引用：3難度：0.8
解析
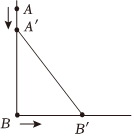4．如圖，在墻角有一根長1米的直木棒AB緊貼墻面，墻面與底面垂直．在t=0s時，木棒的端點A以0.1m/s的速度豎直向下勻速運動，端點B向右沿直線運動，則端點B在t=5s這一時刻的瞬時速度為（　　）
A．
3
30
m
/
s
B．
5
30
m
/
s
C．
3
10
m
/
s
D．
5
10
m
/
s
組卷：38引用：2難度：0.8
解析
5．
A
3
6
-
C
8
10
=（　　）
A．75 B．30 C．-25 D．-70
組卷：71引用：2難度：0.8
解析
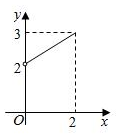6．已知f（x）是定義在[-2，0）∪（0，2]上奇函數，當x＞0時，f（x）的圖象如圖所示，那么f（x）的值域是（　　）
A．[-3，3] B．[-2，2]
C．[-3，-2）∪（2，3] D．（-3，-2]∪[2，3）
組卷：93引用：3難度：0.9
解析
7．已知f（x）和g（x）是定義在R上的函數，且F（x）=f（x）+g（x），則“F（x）有極值點”是“f（x）和g（x）中至少有一個函數有極值點”的（　　）
A．充分不必要條件 B．必要不充分條件
C．充分必要條件 D．既不充分也不必要條件
組卷：100引用：3難度：0.5
解析
8．已知a=2^0.3，b=0.3²，c=log₃0.2，則a、b、c的大小關系是（　　）
A．b＞a＞c B．a＞c＞b C．c＞a＞b D．a＞b＞c
組卷：401引用：4難度：0.8
解析

二、選擇題：本題共4小題，每小題5分，共20分．在每小題給出的選項中，有多項符合題目要求，全部選對的得5分，有選錯的得0分，部分選對的得3分．

9．一曲線族的包絡線（Envelope）是這樣的曲線：該曲線不包含于曲線族中，但過該曲線上的每一點，都有曲線族中的一條曲線與它在這點處相切．下列說法正確的是（　　）

A．若圓

：

是直線ax+by-1=0的包絡線，則有a²+b²=1

B．若曲線C₂是直線族（1-t²）x+2ty-2t-4=0（t∈R）的包絡線，則C₂的長為2π

C．曲線

：

lnx

是三條過點（a,b）的直線的包絡線，其中a＞e則

lna

＜

D．若兩曲線y=x²-1和y=alnx-1是同一條直線的包絡線，則a的取值范圍是（2e,+∞）

組卷：52引用：2難度：0.4

解析

10．甲，乙，丙，丁，戊五人并排站成一排，下列說法正確的是（　　）

A．如果甲，乙必須相鄰且乙在甲的右邊，那么不同的排法有24種

B．最左端只能排甲或乙，最右端不能排甲，則不同的排法共有42種

C．甲乙不相鄰的排法種數為82種

D．甲乙丙按從左到右的順序排列的排法有20種

組卷：417引用：11難度：0.8

解析

11．已知復數z₁，z₂，z₁+z₂在復平面內對應的點分別為A，B，C，且A，B，C不共線，O為復平面的坐標原點．若
z
2
=
z
1
，則（　　）
A．z₁z₂=|z₁|²
B．OA⊥OB
C．四邊形OACB為菱形
D．若z₁-z₂=i（z₁+z₂），則四邊形OACB為正方形
組卷：86引用：1難度：0.7
解析

12．關于函數f（x）=e^x-xsinx-cosx,下列說法中正確的是（　　）

A．曲線y=f（x）在（0，f（0））處的切線方程為y=x

B．函數f（x）在（0，+∞）上無零點

C．x∈（-π，0）時，f（x）有且僅有1個極值點

D．函數f（x）在R上有且僅有1個零點

組卷：44引用：1難度：0.6

解析

三、填空題：本題共4小題，每小題5分，共20分．

13．若函數
g
（
x
）
=
x
2
+
alnx
+
2
x
在[1，2]上是減函數，則實數a的取值范圍是
．
組卷：61引用：2難度：0.6
解析
14．已知
（
1
+
x
）
（
1
-
2
x
）
6
=
a
0
+
a
1
（
x
-
1
）
+
a
2
（
x
-
1
）
2
+
?
+
a
7
（
x
-
1
）
7
，則a₂=
．
組卷：240引用：4難度：0.8
解析
15．函數f（x）=e^xsinx在區間[0，
π
2
]上的值域為

．
組卷：64引用：1難度：0.5
解析
16．已知復數z滿足z-（2-3i）=-1+i,則|z|=
．
組卷：6引用：1難度：0.7
解析

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

17．已知函數f（x）=e^x-ln（x+m）．
（1）當
m
=
1
2
時，求曲線f（x）在點（0，f（0））處切線方程；
（2）當m≤2時，求證：f（x）＞0．
組卷：154引用：2難度：0.4
解析
18．（1）求拋物線y=4x²在點（1，4）處的切線方程；
（2）求曲線
y
=
sinx
x
在點M（π，0）處的切線的斜率．
組卷：31引用：1難度：0.9
解析
19．從5個男生，4個女生中選出4人參加植樹節活動．
（1）共有多少種不同的選取方法？
（2）若至少要選出1個男生，且男生甲和女生乙不能同去，則共有多少種不同的選取方法？
（3）若恰選出2名女生，且4人需要排隊前往，但女生必須相鄰，則共有多少種不同的列？
組卷：60引用：2難度：0.5
解析
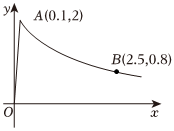20．為了預防流感，某學校對教室進行藥熏消毒．室內每立方米空氣的含藥量y（單位：毫克）隨時間x（單位：h）的變化情況如圖所示，在藥物釋放過程中，y與x成正比（對應圖中OA）；藥物釋放完畢后，y與x函數關系式為y=k?（x+a）^-1（k為常數，其圖象經過點B）．根據圖中提供的信息，回答下列問題：
（1）寫出從藥物釋放開始，y與x之間的函數關系式；
（2）據測定，當空氣中每立方米的含藥量降低到0.25毫克以下時，學生方可進教室．學校每天19：00準時對教室進行藥熏消毒，那么第二天6：30后，學生能否進教室？并說明理由．
組卷：42引用：2難度：0.5
解析
21．已知
（
2
x
-
1
x
）
n
展開式中第3項和第7項的二項式系數相等．
（1）求展開式中含x²的項的系數；
（2）展開式系數的絕對值最大的項是第幾項？
組卷：120引用：1難度：0.7
解析
22．已知函數f（x）=lnx+ax²+（a+2）x.
（1）若a=0，求函數f（x）在點（1，f（1））處的切線方程；
（2）討論f（x）的單調性．
組卷：60引用：3難度：0.6
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．（cosx）'=sinx	B．（3^x）′=3^x
C．（xe^x）′=（x+1）e^x	D．（ lnx x ） ′ = 1 - lnx x

A．[-3，3]	B．[-2，2]
C．[-3，-2）∪（2，3]	D．（-3，-2]∪[2，3）

A．充分不必要條件	B．必要不充分條件
C．充分必要條件	D．既不充分也不必要條件

2020-2021學年福建省寧德市部分達標中學高二（下）期中數學試卷

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

1．對于二項式（2x-x3）7，四位同學作出了四種判斷：①在展開式中沒有常數項；②在展開式中存在常數項；③在展開式中沒有x的一次項；④在展開式中存在x的一次項上述判斷中正確的是（ ）

2．下列求導運算中，正確的是（ ）

3．復數z=a2+a+（a2-a）i為純虛數，則實數a的值是（ ）

4．如圖，在墻角有一根長1米的直木棒AB緊貼墻面，墻面與底面垂直．在t=0s時，木棒的端點A以0.1m/s的速度豎直向下勻速運動，端點B向右沿直線運動，則端點B在t=5s這一時刻的瞬時速度為（ ）

5．A36-C810=（ ）

6．已知f（x）是定義在[-2，0）∪（0，2]上奇函數，當x＞0時，f（x）的圖象如圖所示，那么f（x）的值域是（ ）

7．已知f（x）和g（x）是定義在R上的函數，且F（x）=f（x）+g（x），則“F（x）有極值點”是“f（x）和g（x）中至少有一個函數有極值點”的（ ）

8．已知a=20.3，b=0.32，c=log30.2，則a、b、c的大小關系是（ ）

二、選擇題：本題共4小題，每小題5分，共20分．在每小題給出的選項中，有多項符合題目要求，全部選對的得5分，有選錯的得0分，部分選對的得3分．

9．一曲線族的包絡線（Envelope）是這樣的曲線：該曲線不包含于曲線族中，但過該曲線上的每一點，都有曲線族中的一條曲線與它在這點處相切．下列說法正確的是（ ）

10．甲，乙，丙，丁，戊五人并排站成一排，下列說法正確的是（ ）

11．已知復數z1，z2，z1+z2在復平面內對應的點分別為A，B，C，且A，B，C不共線，O為復平面的坐標原點．若z2=z1，則（ ）

12．關于函數f（x）=ex-xsinx-cosx,下列說法中正確的是（ ）

三、填空題：本題共4小題，每小題5分，共20分．

13．若函數g（x）=x2+alnx+2x在[1，2]上是減函數，則實數a的取值范圍是 ．

14．已知（1+x）（1-2x）6=a0+a1（x-1）+a2（x-1）2+?+a7（x-1）7，則a2=．

15．函數f（x）=exsinx在區間[0，π2]上的值域為 ．

16．已知復數z滿足z-（2-3i）=-1+i,則|z|=．

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

17．已知函數f（x）=ex-ln（x+m）．（1）當m=12時，求曲線f（x）在點（0，f（0））處切線方程；（2）當m≤2時，求證：f（x）＞0．

18．（1）求拋物線y=4x2在點（1，4）處的切線方程；（2）求曲線y=sinxx在點M（π，0）處的切線的斜率．

21．已知（2x-1x）n展開式中第3項和第7項的二項式系數相等．（1）求展開式中含x2的項的系數；（2）展開式系數的絕對值最大的項是第幾項？

22．已知函數f（x）=lnx+ax2+（a+2）x.（1）若a=0，求函數f（x）在點（1，f（1））處的切線方程；（2）討論f（x）的單調性．

1．對于二項式
（
2
x
-
x
3
）
7
，四位同學作出了四種判斷：
①在展開式中沒有常數項；
②在展開式中存在常數項；
③在展開式中沒有x的一次項；
④在展開式中存在x的一次項
上述判斷中正確的是（　　）

2．下列求導運算中，正確的是（　　）

3．復數z=a²+a+（a²-a）i為純虛數，則實數a的值是（　　）

4．如圖，在墻角有一根長1米的直木棒AB緊貼墻面，墻面與底面垂直．在t=0s時，木棒的端點A以0.1m/s的速度豎直向下勻速運動，端點B向右沿直線運動，則端點B在t=5s這一時刻的瞬時速度為（　　）

5．
A
3
6
-
C
8
10
=（　　）

6．已知f（x）是定義在[-2，0）∪（0，2]上奇函數，當x＞0時，f（x）的圖象如圖所示，那么f（x）的值域是（　　）

7．已知f（x）和g（x）是定義在R上的函數，且F（x）=f（x）+g（x），則“F（x）有極值點”是“f（x）和g（x）中至少有一個函數有極值點”的（　　）

8．已知a=2^0.3，b=0.3²，c=log₃0.2，則a、b、c的大小關系是（　　）

9．一曲線族的包絡線（Envelope）是這樣的曲線：該曲線不包含于曲線族中，但過該曲線上的每一點，都有曲線族中的一條曲線與它在這點處相切．下列說法正確的是（　　）

10．甲，乙，丙，丁，戊五人并排站成一排，下列說法正確的是（　　）

11．已知復數z₁，z₂，z₁+z₂在復平面內對應的點分別為A，B，C，且A，B，C不共線，O為復平面的坐標原點．若
z
2
=
z
1
，則（　　）

12．關于函數f（x）=e^x-xsinx-cosx,下列說法中正確的是（　　）

13．若函數
g
（
x
）
=
x
2
+
alnx
+
2
x
在[1，2]上是減函數，則實數a的取值范圍是
．

14．已知
（
1
+
x
）
（
1
-
2
x
）
6
=
a
0
+
a
1
（
x
-
1
）
+
a
2
（
x
-
1
）
2
+
?
+
a
7
（
x
-
1
）
7
，則a₂=
．

15．函數f（x）=e^xsinx在區間[0，
π
2
]上的值域為

．

16．已知復數z滿足z-（2-3i）=-1+i,則|z|=
．

17．已知函數f（x）=e^x-ln（x+m）．
（1）當
m
=
1
2
時，求曲線f（x）在點（0，f（0））處切線方程；
（2）當m≤2時，求證：f（x）＞0．

18．（1）求拋物線y=4x²在點（1，4）處的切線方程；
（2）求曲線
y
=
sinx
x
在點M（π，0）處的切線的斜率．

21．已知
（
2
x
-
1
x
）
n
展開式中第3項和第7項的二項式系數相等．
（1）求展開式中含x²的項的系數；
（2）展開式系數的絕對值最大的項是第幾項？

22．已知函數f（x）=lnx+ax²+（a+2）x.
（1）若a=0，求函數f（x）在點（1，f（1））處的切線方程；
（2）討論f（x）的單調性．