2023-2024學年遼寧省沈陽市郊聯體高一(下)聯考數學試卷(4月份)
發布:2025/6/29 6:0:13
一、單項選擇題(本題共8小題,每小題5分,共40分.在每小題給出的選項中,只有一個選項符合題目要求.)
-
1.函數
的最大值與最小值的和為( )f(x)=cosx(sinx+3cosx),x∈[0,π4]A. 1+32B. 3+232C. 3+332D.3 組卷:79引用:2難度:0.8 -
2.設a=log54,則
,c=0.5-0.2,則a,b,c的大小關系是( )b=log1513A.a<b<c B.b<a<c C.c<b<a D.c<a<b 組卷:2320引用:14難度:0.7 -
3.將函數f(x)=cosx的圖像先向右平移
個單位長度,再把所得函數圖像上的每個點的橫坐標都變為原來的π3倍,縱坐標不變,得到函數g(x)的圖像,若函數g(x)在(-π,0)上單調遞增,則ω的取值范圍是( )1ω(ω>0)A. (0,16]B. (0,23]C. (0,13)D.(0,1] 組卷:268引用:5難度:0.5 -
4.“sinα=1”是“
”的( )α=π2A.充分不必要條件 B.必要不充分條件 C.充分必要條件 D.既不充分又不必要條件 組卷:64引用:4難度:0.9 -
5.已知函數f(x)=|sinx|+cosx,則下列說法正確的是 ( )
①函數f(x)圖象的一條對稱軸的方程為x=2020π;
②函數f(x)在閉區間上單調遞增;[π,74π]
③函數f(x)圖象的一個對稱中心為點;(π2,0)
④函數f(x)的值域為.[-2,2]A.①② B.③④ C.①③ D.②④ 組卷:110引用:1難度:0.5 -
6.設x∈R,則“-2<x<2”是“1<x<2”的( )
A.充分不必要條件 B.必要不充分條件 C.充要條件 D.既不充分也不必要條件 組卷:251引用:4難度:0.9 -
7.已知函數f(x)=
,若函數g(x)=f(x)-a有3個零點,則a的取值范圍是( )|3x+1-1|,x≤0lnx,x>0A.(0,1) B.(0,2] C.(2,+∞) D.(1,+∞) 組卷:536引用:5難度:0.5 -
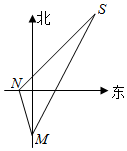 8.如圖,一貨輪航行到M處,測得燈塔S在貨輪的北偏東30°,與燈塔S相距,隨后貨輪按北偏西150的方向航行30min后到達N處,此時測得燈塔在貨輪的東北方向,則貨輪的速度為( )303nmile
8.如圖,一貨輪航行到M處,測得燈塔S在貨輪的北偏東30°,與燈塔S相距,隨后貨輪按北偏西150的方向航行30min后到達N處,此時測得燈塔在貨輪的東北方向,則貨輪的速度為( )303nmileA. 20(6-2)nmile/hB. 20(6+2)nmile/hC. 30(6-2)nmile/hD. 30(6+2)nmile/h組卷:74引用:1難度:0.5
二、多項選擇題(本題共3小題,每小題6分,共18分.在每小題給出的選項中,有多個選項符合題目要求,全部選對的得6分,部分選對的得部分分,有選錯的得0分)
-
9.給出下列命題,其中假命題為( )
A.兩個具有共同終點的向量,一定是共線向量 B.若A,B,C,D是不共線的四點,則 =AB是四邊形ABCD為平行四邊形的充要條件DCC.若 與a同向,且|b|>|a|,則b>abD.λ,μ為實數,若λ =μa,則b與a共線b組卷:94引用:4難度:0.7 -
10.已知函數
,下列選項正確的是( )f(x)=(x+1)ex,x<0(x+1)2ex,x≥0A.函數f(x)在(-2,1)上單調遞增 B.函數f(x)的值域為 [-1e2,+∞)C.若關于x的方程[f(x)]2-a|f(x)|=0有3個不相等的實數根,則實數a的取值范圍是 (1e2,4e)D.不等式f(x)-ax-a>0在(-1,+∞)恰有兩個整數解,則實數a的取值范圍是 [3e2,2e)組卷:137引用:10難度:0.5 -
11.將函數
的圖像上所有點的橫坐標變為原來的ω(ω>0)倍,縱坐標不變,得到的函數圖像恰與函數f(x)=sin(2x+φ)(0<φ<π)的圖像重合,則( )y=cos(x-π6)A.ω=2 B.φ= π3C.直線x= 是曲線y=f(x)的對稱軸π6D.點 是曲線y=f(x)的對稱中心(π3,0)組卷:87引用:3難度:0.6
三、填空題(本題共3小題,每小題5分,共15分.請把正確答案填在題中橫線上)
-
12.若函數f(x)=x3-3x+m在[0,2]上有零點,則實數m的取值范圍為.
組卷:5引用:1難度:0.6 -
13.已知扇形弧長為20cm,圓心角為100°,則該扇形的面積為 cm2.
組卷:100引用:3難度:0.8 -
14.設向量
不平行,向量a,b與2a+b平行,則實數λ=.λa-3b組卷:126引用:1難度:0.7
四、解答題(本題共5小題,共77分.解答應寫出文字說明、證明過程或演算步驟)
-
15.已知函數
.f(x)=sinxcosx-3cos2x+32
(1)求函數f(x)的最小正周期和單調減區間;
(2)求不等式的解集.f(x)≥12組卷:567引用:3難度:0.7 -
16.已知O為△ABC內一點,且滿足
,延長AO交BC于點D.記OA+2OB+3OC=0,AB=a.AC=b
(1)試用,a表示b;AO
(2)求.|BD||DC|組卷:112引用:2難度:0.5 -
17.已知sinα+cosβ=
,cosα+sinβ=-23,求sin(α+β).12組卷:61引用:1難度:0.9 -
18.已知sinx+2cosx=0.
(1)求tanx的值;
(2)求的值.3sinx-cosx3sinx+cosx組卷:46引用:2難度:0.7 -
19.已知函數
.f(x)=sinxcosx-3cos2x+32
(1)求函數f(x)的單調遞減區間;
(2)將函數f(x)的圖象上所有點的橫坐標伸長為原來的2倍,縱坐標不變,再將所得圖象向左平移個單位,得到函數g(x)的圖象,當π6時,求函數g(x)的取值范圍.x∈[π2,π]組卷:399引用:4難度:0.7


