當前位置：試卷中心 > 試卷詳情

2022年廣西高考數學試卷（文科）（甲卷）

發布：2025/6/29 7:0:12

一、選擇題：本題共12小題，每小題5分，共60分。在每小題給出的四個選項中，只有一項是符合題目要求的。

1．在三棱錐P-ABC中，已知△ABC是邊長為8的等邊三角形，PA⊥平面ABC，PA=14，則AB與平面PBC所成角的正弦值為（　　）
A．
7
183
122
B．
793
122
C．
5
183
122
D．
61
122
組卷：289引用：4難度：0.5
解析
2．函數y=xlnx的導數為y′=（　　）
A．x B．1+lnx C．1+xlnx D．1
組卷：83引用：4難度：0.9
解析
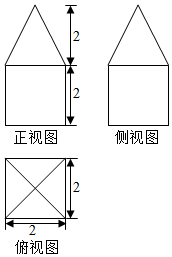3．某幾何體的三視圖如圖所示（單位：cm），則該幾何體的體積是（　　）
A．8 cm³ B．12 cm³ C．
32
3
cm³ D．
40
3
cm³
組卷：47引用：7難度：0.9
解析
4．為慶祝中國共產黨成立100周年，深入推進黨史學習教育，某中學黨支部組織學校初、高中兩個學部的黨員參加了全省教育系統的黨史知識競賽活動，其中初中部20名黨員競賽成績的平均分為a,方差為2；高中部50名黨員競賽成績的平均分為b,方差為
14
5
．若a=b,則該學校全體參賽黨員競賽成績的方差為（　　）
A．
336
35
B．
21
10
C．
12
5
D．
18
7
組卷：121引用：4難度：0.7
解析
5．設集合A={x|y=lg（3-2x）}，集合B={x|y=
1
-
x
}，則A∩B=（　　）
A．
[
1
，
3
2
）
B．（-∞，1] C．
（
-
∞
，
3
2
]
D．
（
3
2
，
+
∞
）
組卷：69引用：8難度：0.9
解析
6．已知指數函數y=a^x是減函數，若m=a²，n=2^a，p=log_a2，則m,n,p的大小關系是（　　）
A．m＞n＞p B．n＞m＞p C．n＞p＞m D．p＞n＞m
組卷：706引用：7難度：0.7
解析
7．已知橢圓C：
x
2
a
2
+
y
2
b
2
=1（a＞b＞0）上有一異于頂點的點P，A，B分別是橢圓C的左、右頂點，且兩直線PA，PB的斜率的乘積為-
1
2
，則橢圓C的離心率e為（　　）
A．
1
2
B．
2
2
C．
3
2
D．
5
4
組卷：735引用：4難度：0.6
解析
8．函數f（x）=ln|x|+cosx的部分圖象大致為（　　）
A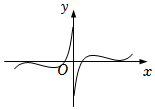． B．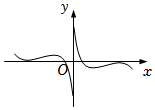
C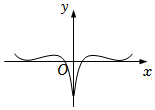． D．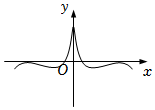
組卷：162引用：3難度：0.8
解析
9．已知正四棱錐底面正方形邊長為4cm,高與斜高夾角為45°，則正四棱錐的體積為（　　）
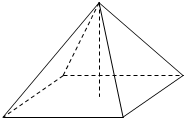
A．32 B．
32
3
C．
8
3
D．
32
2
3
組卷：28引用：1難度：0.7
解析
10．已知復數z=
5
2
+
i
，則其共軛復數
z
=（　　）
A．2+i B．2-i C．10+5i D．10-5i
組卷：98引用：2難度：0.8
解析
11．將函數
y
=
3
cos
（
1
2
x
-
π
3
）
的圖象向左平移
1
8
個周期后所得圖象對應的函數為（　　）
A．
y
=
3
cos
（
1
2
x
-
7
π
12
）
B．
y
=
3
cos
（
1
2
x
+
π
12
）
C．
y
=
3
cos
（
1
2
x
-
5
π
6
）
D．
y
=
3
cos
（
1
2
x
-
π
12
）
組卷：77引用：2難度：0.7
解析
12．設20件產品中有5件不合格，從中任意取出2件，在所取得的產品中發現有一件不合格品，求另一件也是不合格品的概率為（　　）
A．
1
19
B．
17
38
C．
4
19
D．
2
17
組卷：10引用：1難度：0.7
解析

二、填空題：本題共4小題，每小題5分，共20分。

13．已知直線l：y=2x-10與雙曲線
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的一條漸近線平行，且經過雙曲線的一個焦點，則雙曲線的標準方程為
．
組卷：174引用：3難度：0.6
解析
14．圓心在直線2x-y-7=0上的圓C與y軸交于兩點A（0，-4）、B（0，-2），則圓C的方程為
．
組卷：720引用：51難度：0.7
解析
15．若
a
=（1，2，3），
b
=（2，m,3m），
a
⊥
b
，則m=
．
組卷：58引用：1難度：0.7
解析
16．《易經》中記載著一種幾何圖形--八封圖，圖中正八邊形代表八卦，中間的圓代表陰陽太極圖，圖中八塊面積相等的曲邊梯形代表八卦田．某中學開展勞動實習，去測量當地八卦田的面積如圖，現測得正八邊形的過長為8m,代表陰陽太極圖的圓的半徑為2m,則每塊八卦田的面積為
m²．
組卷：94引用：4難度：0.6
解析

三、解答題：共70分。解答應寫出文字說明、證明過程或演算步驟。第17～21題為必考題，每個試題考生都必須作答。第22、23題為選考題，考生根據要求作答。（一）必考題：共60分。

17．閱讀下面題目及其解答過程．
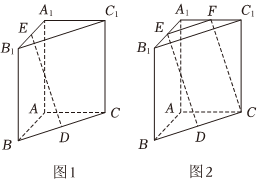
如圖1，在直三棱柱ABC-A₁B₁C₁中，AB⊥AC，D，E分別為BC，A₁B₁的中點．

（1）求證：DE∥平面A₁ACC₁；
（2）求證：AB⊥DE．
解：（1）取A₁C₁的中點F，連接EF，FC，如圖2所示．
在△A₁B₁C₁中，E，F分別為A₁B₁，A₁C₁的中點，
所以EF∥B₁C₁，
EF
=
1
2
B
1
C
1
．
由題意知，四邊形B₁BCC₁為①．
因為D為BC的中點，所以DC∥B₁C₁，
DC
=
1
2
B
1
C
1
．
所以EF∥DC，EF=DC．
所以四邊形DCFE為平行四邊形，
所以DE∥CF．
又②，CF?平面A₁ACC₁，
所以，DE∥平面A₁ACC₁．
（2）因為ABC-A₁B₁C₁為直三棱柱，所以A₁A⊥平面ABC．
又AB?平面ABC，所以③．
因為AB⊥AC，且A₁A⊥AC=A，所以④．
又CF?平面A₁ACC₁，所以AB⊥CF．
因為⑤，所以AB⊥DE．
以上題目的解答過程中，設置了①～⑤五個序號，如下的表格中為每個序號給出了兩個選項，其中只有一個符合邏輯推理．請選出符合邏輯推理的選項（只需填寫“A”或“B”）．

序號選項

① A．矩形????????B．梯形

② A．DE?平面A₁ACC₁??B．DE?平面A₁ACC₁

③ A．BC⊥A₁A??????B．AB⊥A₁A

④ A．AB⊥平面A₁ACC₁??B．BC⊥平面A₁ACC₁

⑤ A．DE=CF???????B．DE∥CF

組卷：59引用：2難度：0.7

解析

18．青少年時期是視覺發育的敏感期與關鍵期，這個階段的視覺發育容易受環境因素影響，某校為研究學生每天使用手機時長與近視率的關系，從全校學生中隨機抽取600名學生進行不記名問卷調查，得到如下數據：有20%的學生每天使用手機超過1h,這些人的近視率為50%；每天使用手機不超過1h的學生的近視率為37.5%．
（1）若從該校學生中隨機抽取一人，請根據以上數據估計該同學近視的概率；
（2）請完成2×2列聯表．并根據調查數據回答：在犯錯誤的概率不超過5%的前提下．可以認為該校學生每天使用手機時長與近視有關嗎？

視力每天使用手機時長合計

超過1h 不超過1h

近視 ___ _ _

不近視 _ _ _

合計 _ ___ 600

附：
χ
2
=
n
（
ad
-
bc
）
2
（
a
+
b
）
（
c
+
d
）
（
a
+
c
）
（
b
+
d
）
．
下表是χ²獨立性檢驗中幾個常用的小概率值和相應的臨界值：

α=P（χ²＞k） 0.1 0.05 0.01 0.005 0.001

k 2.706 3.841 6.635 7.879 10.828

組卷：21引用：2難度：0.6

解析

19．已知等差數列{a_n}的前四項和為10，且a₂，a₃，a₇成等比數列．
（1）求數列{a_n}通項公式；
（2）設
b
n
=
a
n
+
2
n
，求數列{b_n}的前n項和S_n．
組卷：495引用：12難度：0.7
解析
20．設a,b為正數，且a+b=1．證明：
（1）
a
b
+
b
a
≤
2
2
；
（2）（a²+b）（b²+a）＞a²．
組卷：33引用：1難度：0.7
解析
21．在平面直角坐標系xOy中，直線l的參數方程為
x
=
3
2
t
,
y
=
1
2
t
（t為參數），以O為極點，x軸的正半軸為極軸建立極坐標系，曲線C的極坐標方程為ρ²+8ρ²sin²θ-9=0．
（Ⅰ）求直線l的極坐標方程；
（Ⅱ）若直線l與曲線C交于A，B兩點，求|OA|+|OB|的值．
組卷：44引用：1難度：0.6
解析

（二）選考題：共10分。請考生在第22、23題中任選一題作答。如果多做，則按所做的第一題計分。[選修4-4：坐標系與參數方程]（10分）

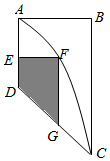22．現有一塊大型的廣告宣傳版面，其形狀是如圖所示的直角梯形ABCD．某廠家因產品宣傳的需要，擬出資規劃出一塊區域（圖中陰影部分）為產品做廣告，形狀為直角梯形DEFG（點F在曲線段AC上，點E在線段AD上）．已知BC=12cm,AB=AD=6cm,其中曲線段AC是以A為頂點，AD為對稱軸的拋物線的一部分．
（Ⅰ）建立適當的平面直角坐標系，分別求出曲線段AC與線段DC的方程；
（Ⅱ）求該廠家廣告區域DEFG的最大面積．
組卷：26引用：8難度：0.3
解析

[選修4-5：不等式選講]（10分）

23．已知a∈R，函數f（x）=ln（1+x）+a?xe^-x．
（1）若a=1，求曲線y=f（x）在（0，f（0））處的切線方程；
（2）若a＞0，且f（x）在其定義域上恰有一個駐點x=x₀，求x₀；
（3）若f（x）在區間（-1，0）上沒有零點，證明：f（x）在區間（0，+∞）上也沒有零點．
組卷：142引用：1難度：0.3
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A． y = 3 cos （ 1 2 x - 7 π 12 ）	B． y = 3 cos （ 1 2 x + π 12 ）
C． y = 3 cos （ 1 2 x - 5 π 6 ）	D． y = 3 cos （ 1 2 x - π 12 ）

序號	選項
①	A．矩形????????B．梯形
②	A．DE?平面A₁ACC₁??B．DE?平面A₁ACC₁
③	A．BC⊥A₁A??????B．AB⊥A₁A
④	A．AB⊥平面A₁ACC₁??B．BC⊥平面A₁ACC₁
⑤	A．DE=CF???????B．DE∥CF

視力	每天使用手機時長		合計
視力	超過1h	不超過1h	合計
近視	_____	_____	_____
不近視	_____	_____	_____
合計	_____	_____	600

α=P（χ²＞k）	0.1	0.05	0.01	0.005	0.001
k	2.706	3.841	6.635	7.879	10.828

2022年廣西高考數學試卷（文科）（甲卷）

一、選擇題：本題共12小題，每小題5分，共60分。在每小題給出的四個選項中，只有一項是符合題目要求的。

1．在三棱錐P-ABC中，已知△ABC是邊長為8的等邊三角形，PA⊥平面ABC，PA=14，則AB與平面PBC所成角的正弦值為（ ）

2．函數y=xlnx的導數為y′=（ ）

3．某幾何體的三視圖如圖所示（單位：cm），則該幾何體的體積是（ ）

5．設集合A={x|y=lg（3-2x）}，集合B={x|y=1-x}，則A∩B=（ ）

6．已知指數函數y=ax是減函數，若m=a2，n=2a，p=loga2，則m,n,p的大小關系是（ ）

7．已知橢圓C：x2a2+y2b2=1（a＞b＞0）上有一異于頂點的點P，A，B分別是橢圓C的左、右頂點，且兩直線PA，PB的斜率的乘積為-12，則橢圓C的離心率e為（ ）

8．函數f（x）=ln|x|+cosx的部分圖象大致為（ ）

9．已知正四棱錐底面正方形邊長為4cm,高與斜高夾角為45°，則正四棱錐的體積為（ ）

10．已知復數z=52+i，則其共軛復數z=（ ）

11．將函數y=3cos（12x-π3）的圖象向左平移18個周期后所得圖象對應的函數為（ ）

12．設20件產品中有5件不合格，從中任意取出2件，在所取得的產品中發現有一件不合格品，求另一件也是不合格品的概率為（ ）

二、填空題：本題共4小題，每小題5分，共20分。

13．已知直線l：y=2x-10與雙曲線x2a2-y2b2=1（a＞0，b＞0）的一條漸近線平行，且經過雙曲線的一個焦點，則雙曲線的標準方程為 ．

14．圓心在直線2x-y-7=0上的圓C與y軸交于兩點A（0，-4）、B（0，-2），則圓C的方程為．

15．若a=（1，2，3），b=（2，m,3m），a⊥b，則m=．

三、解答題：共70分。解答應寫出文字說明、證明過程或演算步驟。第17～21題為必考題，每個試題考生都必須作答。第22、23題為選考題，考生根據要求作答。（一）必考題：共60分。

19．已知等差數列{an}的前四項和為10，且a2，a3，a7成等比數列．（1）求數列{an}通項公式；（2）設bn=an+2n，求數列{bn}的前n項和Sn．

20．設a,b為正數，且a+b=1．證明：（1）ab+ba≤22；（2）（a2+b）（b2+a）＞a2．

（二）選考題：共10分。請考生在第22、23題中任選一題作答。如果多做，則按所做的第一題計分。[選修4-4：坐標系與參數方程]（10分）

[選修4-5：不等式選講]（10分）

1．在三棱錐P-ABC中，已知△ABC是邊長為8的等邊三角形，PA⊥平面ABC，PA=14，則AB與平面PBC所成角的正弦值為（　　）

2．函數y=xlnx的導數為y′=（　　）

3．某幾何體的三視圖如圖所示（單位：cm），則該幾何體的體積是（　　）

5．設集合A={x|y=lg（3-2x）}，集合B={x|y=
1
-
x
}，則A∩B=（　　）

6．已知指數函數y=a^x是減函數，若m=a²，n=2^a，p=log_a2，則m,n,p的大小關系是（　　）

7．已知橢圓C：
x
2
a
2
+
y
2
b
2
=1（a＞b＞0）上有一異于頂點的點P，A，B分別是橢圓C的左、右頂點，且兩直線PA，PB的斜率的乘積為-
1
2
，則橢圓C的離心率e為（　　）

8．函數f（x）=ln|x|+cosx的部分圖象大致為（　　）

9．已知正四棱錐底面正方形邊長為4cm,高與斜高夾角為45°，則正四棱錐的體積為（　　）

10．已知復數z=
5
2
+
i
，則其共軛復數
z
=（　　）

11．將函數
y
=
3
cos
（
1
2
x
-
π
3
）
的圖象向左平移
1
8
個周期后所得圖象對應的函數為（　　）

12．設20件產品中有5件不合格，從中任意取出2件，在所取得的產品中發現有一件不合格品，求另一件也是不合格品的概率為（　　）

13．已知直線l：y=2x-10與雙曲線
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的一條漸近線平行，且經過雙曲線的一個焦點，則雙曲線的標準方程為
．

14．圓心在直線2x-y-7=0上的圓C與y軸交于兩點A（0，-4）、B（0，-2），則圓C的方程為
．

15．若
a
=（1，2，3），
b
=（2，m,3m），
a
⊥
b
，則m=
．

19．已知等差數列{a_n}的前四項和為10，且a₂，a₃，a₇成等比數列．
（1）求數列{a_n}通項公式；
（2）設
b
n
=
a
n
+
2
n
，求數列{b_n}的前n項和S_n．

20．設a,b為正數，且a+b=1．證明：
（1）
a
b
+
b
a
≤
2
2
；
（2）（a²+b）（b²+a）＞a²．