2018-2019學年吉林省白城市通榆一中高三(上)期中數學試卷(理科)
發布:2025/6/29 8:0:17
一、選擇題(共12題,每題5分,共60分)
-
1.已知四邊形ABCD滿足
?AB>0,BC?BC>0,CD?CD,DA>0?DA>0,則四邊形為( )ABA.平行四邊形 B.梯形 C.平面四邊形 D.空間四邊形 組卷:92引用:4難度:0.9 -
2.如果不等式|x-a|<1成立的充分不必要條件是
,則實數a的取值范圍是( )12<x<32A. 12<a<32B. 12≤a≤32C. 或a>32a<12D. 或a≥32a≤12組卷:707引用:29難度:0.9 -
3.已知函數f(x)是定義在[-3,3]上的偶函數,且在[0,3]上單調遞減,則( )
A.f(0)=0 B.f(-3)<f(2) C.f-4)=f(4) D.|f(x)|在[0,3]上單調遞減 組卷:22引用:1難度:0.7 -
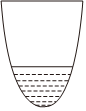 4.將水注入如圖所示的玻璃容器中,從空瓶到注滿,單位時間內進水量相同,能正確反映該玻璃容
4.將水注入如圖所示的玻璃容器中,從空瓶到注滿,單位時間內進水量相同,能正確反映該玻璃容
器中水面的高度與時間關系的圖象是( )A. 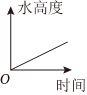
B. 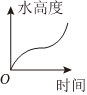
C. 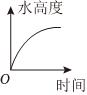
D. 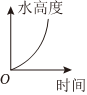 組卷:5引用:2難度:0.7
組卷:5引用:2難度:0.7 -
5.下列命題中是全稱量詞命題并且是真命題的是( )
A.?x∈R,x2+2x+1>0 B.?x∈N,使得2x為偶數 C.所有菱形的四條邊都相等 D.π是無理數 組卷:117引用:4難度:0.8 -
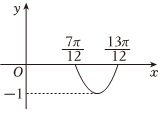 6.已知函數f(x)=cos(ωx+φ)(ω>0,|φ|<π)的部分圖象如圖所示,且存在0≤x1<x2≤π,滿足,則cos(x2-x1)=( )f(x1)=f(x2)=-45
6.已知函數f(x)=cos(ωx+φ)(ω>0,|φ|<π)的部分圖象如圖所示,且存在0≤x1<x2≤π,滿足,則cos(x2-x1)=( )f(x1)=f(x2)=-45A. -35B. 35C. 45D. -45組卷:180引用:3難度:0.8 -
7.已知平面向量
.若a=(1,-3),b=(2,m),則m=( )(a+b)⊥(a-b)A.-1 B.0 C. 23D. -23組卷:218引用:4難度:0.7 -
8.已知向量
=(m2,-9),a=(1,-1),則“m=-3”是“b∥a”的( )bA.充分不必要條件 B.必要不充分條件 C.充要條件 D.既不充分也不必要條件 組卷:300引用:18難度:0.9 -
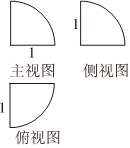 9.如圖,某幾何體三視圖為三個完全相同的圓心角為90°的扇形,則該幾何體的表面積是( )
9.如圖,某幾何體三視圖為三個完全相同的圓心角為90°的扇形,則該幾何體的表面積是( )A. π2B. 3π4C. 5π4D. 7π4組卷:59引用:4難度:0.7 -
10.已知
,a=(15)14,3c+c=0,則( )b=log1415A.a<b<c B.c<a<b C.c<b<a D.a<c<b 組卷:103引用:2難度:0.8 -
11.已知命題p:若α>0,則sinα<α;命題q函數f(x)=2x-x2有兩個零點,則下列說法正確的是( )
①p∧q為真命題;②¬p∨¬q為真命題;③p∨q為真命題;④¬p∨q為真命題A.①② B.①④ C.②③ D.①③④ 組卷:55引用:4難度:0.8 -
12.系統找不到該試題
二、填空題(每題5分,共20分)
-
13.由曲線
以及直線y=1所圍成的封閉圖形的面積是.y=x2,y=14x2組卷:85引用:4難度:0.7 -
14.設m是實數,已知集合 P={(x,y)|(x+2)2+(y-3)2≤4},集合Q={(x,y)|(x+1)2+(y-m)2<
},且P∩Q=Q,則m的取值范圍是 .14組卷:93引用:5難度:0.5 -
15.若函數
在[1,+∞)上是單調減函數,則a的取值范圍是 .f(x)=lnx+ax+1x組卷:19引用:2難度:0.7 -
16.已知平面向量
,則實數m=.a=(m,2),b=(1,m),(a+b)?a=|b|2組卷:17引用:2難度:0.8
三、解答題(17,18、19、20、21、題每題12分22題10分)
-
17.設O為復平面的原點,A,B為單位圓上兩點,A,B所對應的復數分別為z1,z2,z1,z2的輻角的主值分別為α,β.若△AOB的重心G對應的復數為
+13i,求tan(α+β)的值.115組卷:6引用:0難度:0.6 -
18.已知函數f(x)=ax2-ax-xlnx,且f(x)≥0.
(1)求a;
(2)證明:f(x)存在唯一的極大值點x0,且.1e2<f(x0)<14組卷:122引用:2難度:0.4 -
19.已知極坐標系中極點與直角坐標原點均為O,曲線
,C:ρ=12-cosθ.l:θ=π3
(1)求C的直角坐標方程與l和C的交點到O的距離;
(2)已知直線l1:θ=θ0,,l2:θ=θ0+2π3.若l1,l2,l3分別與C交于P,Q,R點,求|OP|+|OQ|+|OR|的最小值.l3:θ=θ0+4π3組卷:1引用:2難度:0.5 -
20.求下列各式的值.
(1)sin105°;
(2)sin(-);5π12
(3)tan15°;
(4)tan.7π12組卷:8引用:1難度:0.7 -
21.已知函數
,且f(x-π)=f(x).f(x)=2sin(ωx-π6)-1(ω>0)
(1)求f(x)的單調遞增區間;
(2)求f(x)在上的最值及其對應x的值.[0,π2]組卷:91引用:3難度:0.7 -
22.在直角坐標系xOy中,直線l的參數方程為
(t為參數).以原點O為極點,x軸正半軸為極軸建立極坐標系,圓C的極坐標方程為ρ2=6ρ(cosθ+sinθ)-14.x=2+22ty=22t
(1)寫出圓C的直角坐標方程;
(2)設直線l與圓C交于A,B兩點,求弦長AB.組卷:131引用:3難度:0.6


