當(dāng)前位置：試卷中心 > 試卷詳情

2023-2024學(xué)年河南省周口市西華第一高級中學(xué)等校高二（上）聯(lián)考數(shù)學(xué)試卷（1月份）

發(fā)布：2025/6/29 10:0:14

一、單項選擇題（共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．）

1．已知向量
a
=
（
1
，
1
，
0
）
，
b
=
（
1
，-
1
，
0
）
，若
（
a
+
λ
b
）
⊥
（
a
+
μ
b
）
，則（　　）
A．λ+μ=1 B．λ+μ=-1 C．λμ=1 D．λμ=-1
組卷：60引用：2難度：0.7
解析
2．如圖，在平行六面體（底面為平行四邊形的四棱柱）ABCD-A₁B₁C₁D₁中，E為BC延長線上一點，
BC
=
3
CE
，則
D
1
E
=（　　）
A．
AB
+
1
3
AD
-
A
A
1
B．
AB
+
AD
-
2
3
A
A
1
C．
AB
+
1
3
AD
+
A
A
1
D．
AB
-
AD
+
1
3
A
A
1
組卷：154引用：2難度：0.8
解析
3．已知F是橢圓
C
：
x
2
2
+
y
2
=
1
的左焦點，P為橢圓C上任意一點，點Q（4，3），則|PQ|+|PF|的最大值為（　　）
A．
5
2
B．
3
2
C．
34
D．
4
2
組卷：1037引用：12難度：0.8
解析
4．若直線x-y+a=0與圓x²+y²=4相交于A，B兩點，且∠AOB=120°（O為坐標(biāo)原點），則|a|=（　　）
A．1 B．
2
C．2 D．
2
2
組卷：198引用：3難度：0.8
解析
5．若直線x+ky-2-3k=0與圓x²+y²=r²（r＞0）相切，則r的最大值為（　　）
A．3 B．
10
C．
2
3
D．
13
組卷：77引用：1難度：0.6
解析
6．已知直線l₁：ax+2y+1=0，l₂：（3-a）x-y+a=0，則條件“a=1”是“l(fā)₁⊥l₂“的（　　）
A．充分必要條件 B．充分不必要條件
C．必要不充分條件 D．既不必要也不充分條件
組卷：287引用：8難度：0.9
解析
7．在等比數(shù)列{a_n}中，a₂=1，a₄?a₈=16，則a₄=（　　）
A．2 B．-2 C．4 D．-4
組卷：243引用：1難度：0.5
解析
8．系統(tǒng)找不到該試題

二、多項選擇題（共4小題，每小題5分，共20分．在每小題給出的四個選項中，有多項是符合題目要求的．）

9．已知雙曲線C：x²-
y
2
3
=1，F(xiàn)₁，F(xiàn)₂為雙曲線的左、右焦點，若直線l過點F₂，且與雙曲線的右支交于M，N兩點，下列說法正確的是（　　）
A．雙曲線C的離心率為
3
B．若l的斜率為2，則MN的中點為（8，12）
C．若∠F₁MF₂=
π
3
，則△MF₁F₂的面積為3
3
D．使△MNF₁為等腰三角形的直線l有3條
組卷：5引用：0難度：0.5
解析
10．已知數(shù)列{a_n}滿足
a
1
=
3
2
，
a
n
+
1
=
3
a
n
6
+
a
n
，則下列結(jié)論中錯誤的有（　　）
A．
{
1
a
n
+
1
3
}
為等比數(shù)列
B．{a_n}的通項公式為
1
3
?
2
n
-
1
-
1
C．{a_n}為遞增數(shù)列
D．
{
1
a
n
}
的前n項和為
2
n
-
n
3
-
1
組卷：48引用：2難度：0.6
解析
11．對于不等關(guān)系人們在早期會使用文字或象征性記號來記述．例如，荷蘭數(shù)學(xué)家吉拉爾在他1629年所著《代數(shù)新發(fā)現(xiàn)》一書中，使用下面記號：AffB表示A大于B，A§B表示A小于B．若affbff0，則下列不等式一定成立的是（　　）
A．（a+b）ff2
ab
B．B．
（
a
+
b
2
）
2
§
a
2
+
b
2
2
C．
a
b
§
a
+
1
b
+
1
D．a(chǎn)c²ffbc²
組卷：23引用：1難度：0.7
解析

12．下列結(jié)論正確的有（　　）

A．若隨機(jī)變量ξ，η滿足η=2ξ+1，則D（η）=2D（ξ）+1

B．若隨機(jī)變量ξ-N（3，σ²），且P（ξ＜6）=0.84，則P（3＜ξ＜6）=0.34

C．若線性相關(guān)系數(shù)|r|越接近1，則兩個變量的線性相關(guān)性越強(qiáng)

D．按從小到大順序排列的兩組數(shù)據(jù)：甲組：27，30，37，m,40，50；乙組：24，n,33，44，48，52，若這兩組數(shù)據(jù)的第30百分位數(shù)、第50百分位數(shù)都分別對應(yīng)相等，則m+n=67

組卷：92引用：4難度：0.7

解析

三、填空題：本題共4小題，每小題5分，共20分．

13．若等差數(shù)列{a_n}的前n項和為S_n，a₂+a₄=14，S₇=70，則數(shù)列{a_n}的通項公式為
．
組卷：49引用：5難度：0.7
解析
14．設(shè)M是橢圓
x
2
a
2
+
y
2
b
2
=1（a＞b＞0）上一點，F(xiàn)₁，F(xiàn)₂為焦點，如果∠MF₁F₂=75°，∠MF₂F₁=15°，則橢圓的離心率

．
組卷：103引用：2難度：0.5
解析
15．過圓x²+y²=5上一點M（1，2）的圓的切線方程為

．
組卷：39引用：6難度：0.5
解析
16．已知拋物線y²=4x的準(zhǔn)線過橢圓
x
2
a
2
+
y
2
2
=
1
的焦點，則橢圓的準(zhǔn)線方程為
．
組卷：48引用：1難度：0.7
解析

四、解答題：本題共6小題，共70分，其中第17題10分，其余均12分。

17．已知橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
，四點
P
1
（
2
，
6
2
）
，
P
2
（
0
，
1
）
P
3
（
1
，
3
2
）
，
P
4
（
1
，-
3
2
）
中恰有三點在橢圓C上．點P為圓M：x²+y²=a²+b²上任意一點，O為坐標(biāo)原點．
（1）求橢圓C及圓M的標(biāo)準(zhǔn)方程；
（2）設(shè)直線l經(jīng)過點P，且與橢圓C相切，與圓M相交于另一點A，點A關(guān)于原點的對稱點為B，試判斷直線PB與橢圓C的位置關(guān)系，并證明你的結(jié)論．
組卷：74引用：7難度：0.6
解析
18．記S_n為的等差數(shù)列{a_n}的前n項和，已知a₁=-9，S₃=-21．
（1）求{a_n}的通項公式；
（2）求S_n的最小值及取得最小值時n的值．
組卷：25引用：3難度：0.7
解析
19．已知數(shù)列{a_n}的前n項和記為A_n，且
A
n
=
n
（
a
1
+
a
n
）
2
，數(shù)列{b_n}是公比為q的等比數(shù)列，它的前n項和記為B_n．若a₁=b₁≠0，且存在不小于3的正整數(shù)m,k,使得a_k=b_m．
（1）若a₁=1，a₃=5，求a₂的值；
（2）求證：數(shù)列{a_n}是等差數(shù)列；
（3）若q=2，是否存在正整數(shù)m,k,使得A_k=65B_m？若存在，求出m,k的值；若不存在，請說明理由．
組卷：65引用：2難度：0.3
解析
20．在數(shù)列{a_n}中，a₁=2，a_n是1與a_na_n+1的等差中項．
（1）求證：數(shù)列
{
1
a
n
-
1
}
是等差數(shù)列；
（2）令
b
n
=
（
-
1
）
n
?
（
3
a
n
-
1
+
1
）
，記數(shù)列{b_n}的前n項和為S_n，求S₁₀₀．
組卷：102引用：1難度：0.5
解析
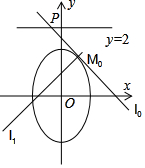21．如圖，已知點M₀（x₀，y₀）是橢圓C：
y
2
2
+
x
2
=1上的動點，以M₀為切點的切線l₀與直線y=2相交于點P．
（1）過點M₀且l₀與垂直的直線為l₁，求l₁與y軸交點縱坐標(biāo)的取值范圍；
（2）在y軸上是否存在定點T，使得以PM₀為直徑的圓恒過點T？若存在，求出點T的坐標(biāo)；若不存在，說明理由．
（參考定理：若點Q（x₁，y₁）在橢圓
y
2
a
2
+
x
2
b
2
=
1
（
a
＞
b
＞
0
）
，則以Q為切點的橢圓的切線方程是：
y
1
y
a
2
+
x
1
x
b
2
=
1
（
a
＞
b
＞
0
）
．
組卷：36引用：3難度：0.5
解析
22．已知點P（4，2）在拋物線C：x²=2py上．
（1）求拋物線C的焦點到其準(zhǔn)線的距離；
（2）設(shè)直線l與C交于A，B兩點，O為坐標(biāo)原點，且∠AOB=90°，求△AOB面積的最小值．
組卷：77引用：2難度：0.6
解析

0/60 進(jìn)入組卷

0/20 進(jìn)入試卷籃

布置作業(yè) 發(fā)布測評 反向細(xì)目表 平行組卷 下載答題卡 試卷分析 在線訓(xùn)練 收藏試卷

充值會員，資源免費下載

A． AB + 1 3 AD - A A 1	B． AB + AD - 2 3 A A 1
C． AB + 1 3 AD + A A 1	D． AB - AD + 1 3 A A 1

A．充分必要條件	B．充分不必要條件
C．必要不充分條件	D．既不必要也不充分條件

A．（a+b）ff2 ab	B．B．（ a + b 2 ） 2 § a 2 + b 2 2
C． a b § a + 1 b + 1	D．a(chǎn)c²ffbc²

2023-2024學(xué)年河南省周口市西華第一高級中學(xué)等校高二（上）聯(lián)考數(shù)學(xué)試卷（1月份）

一、單項選擇題（共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．）

1．已知向量a=（1，1，0），b=（1，-1，0），若（a+λb）⊥（a+μb），則（ ）

2．如圖，在平行六面體（底面為平行四邊形的四棱柱）ABCD-A1B1C1D1中，E為BC延長線上一點，BC=3CE，則D1E=（ ）

3．已知F是橢圓C：x22+y2=1的左焦點，P為橢圓C上任意一點，點Q（4，3），則|PQ|+|PF|的最大值為（ ）

4．若直線x-y+a=0與圓x2+y2=4相交于A，B兩點，且∠AOB=120°（O為坐標(biāo)原點），則|a|=（ ）

5．若直線x+ky-2-3k=0與圓x2+y2=r2（r＞0）相切，則r的最大值為（ ）

6．已知直線l1：ax+2y+1=0，l2：（3-a）x-y+a=0，則條件“a=1”是“l(fā)1⊥l2“的（ ）

7．在等比數(shù)列{an}中，a2=1，a4?a8=16，則a4=（ ）

二、多項選擇題（共4小題，每小題5分，共20分．在每小題給出的四個選項中，有多項是符合題目要求的．）

9．已知雙曲線C：x2-y23=1，F(xiàn)1，F(xiàn)2為雙曲線的左、右焦點，若直線l過點F2，且與雙曲線的右支交于M，N兩點，下列說法正確的是（ ）

10．已知數(shù)列{an}滿足a1=32，an+1=3an6+an，則下列結(jié)論中錯誤的有（ ）

12．下列結(jié)論正確的有（ ）

三、填空題：本題共4小題，每小題5分，共20分．

13．若等差數(shù)列{an}的前n項和為Sn，a2+a4=14，S7=70，則數(shù)列{an}的通項公式為．

14．設(shè)M是橢圓x2a2+y2b2=1（a＞b＞0）上一點，F(xiàn)1，F(xiàn)2為焦點，如果∠MF1F2=75°，∠MF2F1=15°，則橢圓的離心率 ．

15．過圓x2+y2=5上一點M（1，2）的圓的切線方程為 ．

16．已知拋物線y2=4x的準(zhǔn)線過橢圓x2a2+y22=1的焦點，則橢圓的準(zhǔn)線方程為．

四、解答題：本題共6小題，共70分，其中第17題10分，其余均12分。

18．記Sn為的等差數(shù)列{an}的前n項和，已知a1=-9，S3=-21．（1）求{an}的通項公式；（2）求Sn的最小值及取得最小值時n的值．

20．在數(shù)列{an}中，a1=2，an是1與anan+1的等差中項．（1）求證：數(shù)列{1an-1}是等差數(shù)列；（2）令bn=（-1）n?（3an-1+1），記數(shù)列{bn}的前n項和為Sn，求S100．

22．已知點P（4，2）在拋物線C：x2=2py上．（1）求拋物線C的焦點到其準(zhǔn)線的距離；（2）設(shè)直線l與C交于A，B兩點，O為坐標(biāo)原點，且∠AOB=90°，求△AOB面積的最小值．

1．已知向量
a
=
（
1
，
1
，
0
）
，
b
=
（
1
，-
1
，
0
）
，若
（
a
+
λ
b
）
⊥
（
a
+
μ
b
）
，則（　　）

2．如圖，在平行六面體（底面為平行四邊形的四棱柱）ABCD-A₁B₁C₁D₁中，E為BC延長線上一點，
BC
=
3
CE
，則
D
1
E
=（　　）

3．已知F是橢圓
C
：
x
2
2
+
y
2
=
1
的左焦點，P為橢圓C上任意一點，點Q（4，3），則|PQ|+|PF|的最大值為（　　）

4．若直線x-y+a=0與圓x²+y²=4相交于A，B兩點，且∠AOB=120°（O為坐標(biāo)原點），則|a|=（　　）

5．若直線x+ky-2-3k=0與圓x²+y²=r²（r＞0）相切，則r的最大值為（　　）

6．已知直線l₁：ax+2y+1=0，l₂：（3-a）x-y+a=0，則條件“a=1”是“l(fā)₁⊥l₂“的（　　）

7．在等比數(shù)列{a_n}中，a₂=1，a₄?a₈=16，則a₄=（　　）

9．已知雙曲線C：x²-
y
2
3
=1，F(xiàn)₁，F(xiàn)₂為雙曲線的左、右焦點，若直線l過點F₂，且與雙曲線的右支交于M，N兩點，下列說法正確的是（　　）

10．已知數(shù)列{a_n}滿足
a
1
=
3
2
，
a
n
+
1
=
3
a
n
6
+
a
n
，則下列結(jié)論中錯誤的有（　　）

12．下列結(jié)論正確的有（　　）

13．若等差數(shù)列{a_n}的前n項和為S_n，a₂+a₄=14，S₇=70，則數(shù)列{a_n}的通項公式為
．

14．設(shè)M是橢圓
x
2
a
2
+
y
2
b
2
=1（a＞b＞0）上一點，F(xiàn)₁，F(xiàn)₂為焦點，如果∠MF₁F₂=75°，∠MF₂F₁=15°，則橢圓的離心率

．

15．過圓x²+y²=5上一點M（1，2）的圓的切線方程為

．

16．已知拋物線y²=4x的準(zhǔn)線過橢圓
x
2
a
2
+
y
2
2
=
1
的焦點，則橢圓的準(zhǔn)線方程為
．

18．記S_n為的等差數(shù)列{a_n}的前n項和，已知a₁=-9，S₃=-21．
（1）求{a_n}的通項公式；
（2）求S_n的最小值及取得最小值時n的值．

20．在數(shù)列{a_n}中，a₁=2，a_n是1與a_na_n+1的等差中項．
（1）求證：數(shù)列
{
1
a
n
-
1
}
是等差數(shù)列；
（2）令
b
n
=
（
-
1
）
n
?
（
3
a
n
-
1
+
1
）
，記數(shù)列{b_n}的前n項和為S_n，求S₁₀₀．

22．已知點P（4，2）在拋物線C：x²=2py上．
（1）求拋物線C的焦點到其準(zhǔn)線的距離；
（2）設(shè)直線l與C交于A，B兩點，O為坐標(biāo)原點，且∠AOB=90°，求△AOB面積的最小值．