2025年四川省內江市威遠中學高考數學一模試卷
發布:2025/6/29 11:0:14
一、單選題:本題共8個小題,每小題5分,共計40分
-
1.cos30°cos105°-sin30°sin75°=( )
A.- 32B.- 22C. 22D. 32組卷:230引用:1難度:0.7 -
2.已知矩形ABCD中,AB=3,BC=2,將△CBD沿BD折起至△C'BD.當直線C'B與AD所成的角最大時,三棱錐C'-ABD的體積為( )
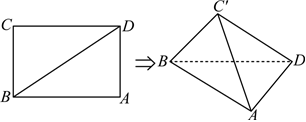
A. 53B. 51313C. 253D. 61313組卷:109引用:3難度:0.5 -
3.已知i為虛數單位,若復數z=
,則|z|=( )3-i1+iA.1 B.2 C. 2D. 5組卷:404引用:6難度:0.8 -
4.已知定義在R上的函數f(x)滿足f(2-x)為奇函數,函數f(x+3)關于直線x=1對稱,則下列式子一定成立的是( )
A.f(x-2)=f(x) B.f(x-2)=f(x+6) C.f(x-2)?f(x+2)=1 D.f(-x)+f(x+1)=0 組卷:256引用:4難度:0.7 -
5.公差不為0的等差數列{an}的前n項和為Sn,若S3=a5-1,a1,a2,a6成等比數列,則Sn=( )
A. 3n2-n2B. n2+n2C.3n-2 D. 5n-3n22組卷:147引用:3難度:0.7 -
 6.如圖,F1,F2分別是雙曲線的左、右焦點,點P是雙曲線與圓x2+y2=a2+b2在第二象限的一個交點,點Q在雙曲線上,且x2a2-y2b2=1(a>0,b>0),則雙曲線的離心率為( )F1P=12F2Q
6.如圖,F1,F2分別是雙曲線的左、右焦點,點P是雙曲線與圓x2+y2=a2+b2在第二象限的一個交點,點Q在雙曲線上,且x2a2-y2b2=1(a>0,b>0),則雙曲線的離心率為( )F1P=12F2QA. 102B. 2C. 3D. 173組卷:322引用:5難度:0.5 -
7.已知平面向量
滿足a,b與|a|=3,|b|=1,a的夾角為b,則實數λ的值為( )30°,(λb-a)⊥aA.-2 B.2 C. -12D. 12組卷:257引用:5難度:0.7 -
8.已知全集U={1,2,3,4},A={x|x2-3x+2=0},則?UA=( )
A.{1} B.{1,2} C.{3,4} D.{1,2,3,4} 組卷:32引用:2難度:0.8
二.多選題:本題共3個小題,每個小題6分,共計18分
-
9.若正實數a,b滿足a+b=1,則下列說法正確的是( )
A. 1a有最小值2+1bB.a2+b2有最大值 12C.ab有最大值 14D. a有最大值+b2組卷:271引用:23難度:0.8 -
10.已知函數
的圖象的一條對稱軸為x=π,其中ω為常數,且ω∈(0,1),則以下結論正確的是( )f(x)=2sin(ωx-π6)A.函數f(x)的最小正周期為 32πB.將函數f(x)的圖象向右平移 個單位所得圖象關于y軸對稱π2C.函數f(x)在區間[ ,-π6]上單調遞增π2D.函數f(x)在區間(0,100π)上有66個零點 組卷:12引用:1難度:0.7 -
11.已知函數f(x)的定義域為R,滿足f(x+2)=
f(x),當x=(0,2]時,f(x)=12對?x∈[m,+∞),下列選項正確的是( )exxA.f(x)≤2e,則m的最小值為-1 B.f(x)≤2e,則m的值不存在 C.f(x)極小值≤2e,則m≥-3 D.m=0時,函數y=f(x)所有極小值之和大于2e 組卷:67引用:1難度:0.5
三.填空題:本題共3個小題,每小題5分,共計15分
-
12.甲、乙、丙、丁4人分別到A、B、C、D四所學校實習,每所學校一人,在甲不去A校的條件下,乙不去B校的概率是 .
組卷:139引用:5難度:0.7 -
13.數字波是由0和1組成的脈沖信號序列,某類信號序列包含有n個數字0和n個數字1,且每個數字0之前1的個數多于0的個數.當n等于3時,這樣的信號序列有 種;當n等于5時,這樣的信號序列有 種.
組卷:24引用:2難度:0.7 -
14.已知拋物線C:y2=4x的焦點為F,直線l:x-y-1=0與拋物線C交于A,B兩點(其中點A在x軸上方),則
=.|AF||FB|組卷:99引用:6難度:0.5
三.解答題:本題共5個小題,共計77分
-
15.已知:集合A={x|3<x≤6},B={x|m≤x≤2m+1}.
(1)若m=2,求A∩B;
(2)若x∈A是x∈B的充分條件,求實數m的取值范圍;
(3)若A∩B=?,求實數m的取值范圍.組卷:170引用:7難度:0.6 -
16.已知等比數列{an}的前n項和為Sn,且an+1=2Sn+9(n∈N*).
(1)求數列{an}的通項公式;
(2)記bn=log3an,證明:.1b1b2+1b2b3+?+1bnbn+1<12組卷:364引用:5難度:0.5 -
17.已知⊙O1:(x+1)2+y2=1,⊙O2:(x-1)2+y2=9,⊙M與⊙O1外切,與⊙O2內切.
(1)求點M的軌跡方程;
(2)若A,B是點M的軌跡上的兩點,O為坐標原點,直線OA,OB的斜率分別為k1,k2,直線AB的斜率存在,△AOB的面積為,證明:k1?k2為定值.3組卷:88引用:5難度:0.5 -
18.在△ABC中,A,B,C的對邊分別為a,b,c,acosB-2acosC=(2c-b)cosA.
(1)若c=a,求cosB的值;3
(2)若b=1,∠BAC的平分線AD交BC于點D,求AD長度的取值范圍.組卷:1732引用:13難度:0.6 -
19.已知函數f(x)=2ex-sin2x.
(1)當x≥0時,求函數f(x)的最小值;
(2)若對于,不等式4xex+xcos2x-ax2-5x≥0恒成立,求實數a的取值范圍.?x∈(-π12,+∞)組卷:39引用:2難度:0.5


