2024-2025學(xué)年東北三省名校聯(lián)盟高三(上)第一次質(zhì)檢數(shù)學(xué)試卷
發(fā)布:2025/6/29 13:0:15
一、選擇題:本題共8小題,每小題5分,共40分.在每小題給出的四個(gè)選項(xiàng)中,只有一項(xiàng)是符合題目要求的.
-
1.下列函數(shù)中,最小正周期是π且在區(qū)間(
,π)上是增函數(shù)的是( )π2A.y=sin2x B.y=sinx C.y=tan x2D.y=cos2x 組卷:17引用:1難度:0.7 -
2.在△ABC中,
,A=π4,AC=4,則BC邊上的高為( )AB=2A. 2105B. 22C.3 D. 23組卷:31引用:4難度:0.7 -
3.等比數(shù)列{an}的前n和Sn=2n-1,則數(shù)列{an}的公比為( )
A. 12B. 13C.2 D.3 組卷:338引用:1難度:0.8 -
4.一艘船以4km/h的速度沿著與水流方向成120°夾角的方向航行,已知河水流速為2km/h,則經(jīng)過
h,該船的實(shí)際航程為( )3A.2 km15B.6 km C.2 km21D.8 km 組卷:557引用:3難度:0.7 -
5.已知
在定義域內(nèi)單調(diào),則a的取值范圍是( )f(x)=(a+2)x,x<1x2-2ax+1,x≥1A.(-1,+∞) B.(-1,0] C.(-1,1] D.[0,1] 組卷:46引用:1難度:0.7 -
6.已知p:x-a>0,q:x>1,若p是q的充分不必要條件,則實(shí)數(shù)a的取值范圍為( )
A.{a|a<1} B.{a|a≤1} C.{a|a>1} D.{a|a≥1} 組卷:50引用:1難度:0.9 -
7.
=( )i(1+i)1-iA.1 B.-1 C.-i D.i 組卷:55引用:2難度:0.9 -
8.系統(tǒng)找不到該試題
二、多選題:本題共3小題,每小題6分,共18分.在每小題給出的選項(xiàng)中,有多項(xiàng)符合題目要求,全部選對(duì)的得6分,部分選對(duì)的得部分分,有選錯(cuò)的得0分.
-
9.已知函數(shù)f(x)的定義域?yàn)镽,且f(x)+f(x+2)=2.若f(x)的圖象關(guān)于點(diǎn)(1,1)對(duì)稱,f(0)=0,則( )
A.f(2)=4 B.f(x)的圖象關(guān)于直線x=2對(duì)稱 C.f(x)=f(x+4) D. f(2k)=125∑k=0組卷:75引用:3難度:0.4 -
10.某次考試后,甲、乙兩班的數(shù)學(xué)老師分別統(tǒng)計(jì)了各自班級(jí)的數(shù)學(xué)成績(百分制,均位于[40,100]內(nèi)),并將所得數(shù)據(jù)分為6組:[40,50),[50,60),…,[90,100],整理得到如圖所示的頻率分布直方圖,則下列說法不正確的是( )
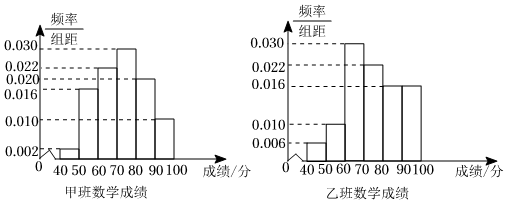
A.甲班數(shù)學(xué)成績的平均分約為72分(同一組中的數(shù)據(jù)用該組區(qū)間的中點(diǎn)值代替) B.乙班數(shù)學(xué)成績的最高分高于甲班數(shù)學(xué)成績的最高分 C.甲班數(shù)學(xué)成績的及格率低于乙班數(shù)學(xué)成績的及格率(成績不低于60分為及格) D.甲班數(shù)學(xué)成績不低于80分的人數(shù)多于乙班數(shù)學(xué)成績不低于80分的人數(shù) 組卷:79引用:2難度:0.8 -
11.對(duì)具有相關(guān)關(guān)系的兩個(gè)變量x和y進(jìn)行回歸分析時(shí),經(jīng)過隨機(jī)抽樣獲得成對(duì)的樣本數(shù)據(jù)(xi,yi)(i=1,2,…,n),則下列說法正確的是( )
A.若兩變量x,y具有線性相關(guān)關(guān)系,則回歸直線至少經(jīng)過一個(gè)樣本點(diǎn) B.變量x,y的線性相關(guān)系數(shù)r的絕對(duì)值越接近1,則兩個(gè)變量y與x的線性相關(guān)程度越強(qiáng) C.用殘差平方和來比較兩個(gè)模型的擬合效果時(shí),殘差平方和越小,模型的擬合效果越好 D.用 來刻畫回歸模型的擬合效果時(shí),若所有樣本點(diǎn)都落在一條斜率為非零的直線上,則R2的值為1R2=1-n∑i=1(yi-y)2n∑i=1(xi-x)2組卷:49引用:3難度:0.7
三、填空題:本題共3小題,每小題5分,共15分.
-
12.函數(shù)y=xlnx的單調(diào)減區(qū)間為.
組卷:60引用:17難度:0.7 -
13.正數(shù)數(shù)列{an}的前n項(xiàng)和為Sn,且存在正數(shù)t,使得對(duì)于任意的正整數(shù)n,都有
成立.若tSn=t+an2,則t的取值范圍是.limn→+∞Snan<t組卷:17引用:2難度:0.5 -
14.已知四面體ABCD的各頂點(diǎn)都在球O的表面上,AB=CD=2
,E,F(xiàn)分別為AB,CD的中點(diǎn),O為EF的中點(diǎn).若AB⊥CD,直線AC與BD所成的角為60°,AB<EF,則球O的表面積為 .2組卷:6引用:2難度:0.5
四、解答題:本題共5小題,共77分.
-
15.數(shù)學(xué)的發(fā)展推動(dòng)著科技的進(jìn)步,5G技術(shù)的蓬勃發(fā)展得益于線性代數(shù)、群論等數(shù)學(xué)知識(shí)的應(yīng)用.目前某區(qū)域市場(chǎng)中5G智能終端產(chǎn)品的制造僅能由H公司和G公司提供技術(shù)支持.據(jù)市場(chǎng)調(diào)研預(yù)測(cè),5G商用初期,該區(qū)域市場(chǎng)中采用H公司與G公司技術(shù)的智能終端產(chǎn)品分別占比a0=5%及b0=95%.假設(shè)兩家公司的技術(shù)更新周期一致,且隨著技術(shù)優(yōu)勢(shì)的體現(xiàn),每次技術(shù)更新后,上一周期采用G公司技術(shù)的產(chǎn)品中有20%轉(zhuǎn)而采用H公司技術(shù),采用H公司技術(shù)的僅有5%轉(zhuǎn)而采用G公司技術(shù).設(shè)第n次技術(shù)更新后,該區(qū)域市場(chǎng)中采用H公司與G公司技術(shù)的智能終端產(chǎn)品占比分別為an及bn,不考慮其他因素的影響.
(1)用an表示an+1,并求實(shí)數(shù)λ,使{an+λ}是等比數(shù)列;
(2)經(jīng)過若干次技術(shù)更新后該區(qū)域市場(chǎng)采用H公司技術(shù)的智能終端產(chǎn)品占比能否超過75%?若能,至少需要經(jīng)過幾次技術(shù)更新?若不能,請(qǐng)說明理由.(參考數(shù)據(jù):lg2≈0.301,lg3≈0.477)組卷:14引用:2難度:0.4 -
16.設(shè)函數(shù)f(x)=[ax2-(5a+1)x+5a+4]ex,a∈R.
(1)當(dāng)a=1時(shí),求函數(shù)f(x)的單調(diào)區(qū)間;
(2)若f(x)在x=3處取得極小值,求a的取值范圍.組卷:100引用:1難度:0.7 -
17.在△ABC中,cosC=
,c=8,再從條件①、條件②這兩個(gè)條件中選擇一個(gè)作為已知,條件①:a=7;條件②:cosB=17.1114
求:(1)b的值;
(2)角A的大小和△ABC的面積.組卷:44引用:1難度:0.7 -
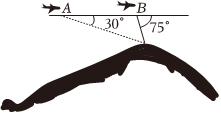 18.如圖,一架直升飛機(jī)的航線和山頂在同一個(gè)鉛直平面內(nèi),已知飛機(jī)的高度為海拔10千米,速度為180千米/小時(shí),飛行員先看到山頂?shù)母┙菫?0°,經(jīng)過2分鐘后又看到山頂?shù)母┙菫?5°,求山頂?shù)暮0胃叨龋?/h2>組卷:26引用:3難度:0.7
18.如圖,一架直升飛機(jī)的航線和山頂在同一個(gè)鉛直平面內(nèi),已知飛機(jī)的高度為海拔10千米,速度為180千米/小時(shí),飛行員先看到山頂?shù)母┙菫?0°,經(jīng)過2分鐘后又看到山頂?shù)母┙菫?5°,求山頂?shù)暮0胃叨龋?/h2>組卷:26引用:3難度:0.7 -
 19.在某中學(xué)舉行的環(huán)保知識(shí)競(jìng)賽中,隨機(jī)抽取x名參賽同學(xué)的成績(得分的整數(shù))進(jìn)行整理后分成五組,繪制出如圖所示的頻率分布直方圖,已知圖中從左到右的第一、第三、第四、第五小組的頻率分別為0.30,0.15,0.10,0.05,第二小組的頻數(shù)為40.
19.在某中學(xué)舉行的環(huán)保知識(shí)競(jìng)賽中,隨機(jī)抽取x名參賽同學(xué)的成績(得分的整數(shù))進(jìn)行整理后分成五組,繪制出如圖所示的頻率分布直方圖,已知圖中從左到右的第一、第三、第四、第五小組的頻率分別為0.30,0.15,0.10,0.05,第二小組的頻數(shù)為40.
(1)求第二小組的頻率,并補(bǔ)全這個(gè)頻率分布直方圖,畫出頻率分布折線圖;
(2)若采用分層抽樣的方法,從樣本中隨機(jī)取20人,則第三組和第四組各抽取多少人?
(3)在(2)的條件下,從第三組和第四組抽取的人中任選取2人,則她們不在同一組別的概率是多少?組卷:8引用:2難度:0.5


