2022-2023學年吉林省長春六中高三（上）期末數學試卷

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求.

• 1．兩個等差數列{a_n}和{b_n}，其前n項和分別為S_n，T_n，且

  S

  n

  T

  n

  =

  7

  n

  +

  2

  n

  +

  3

  ，則

  a

  2

  +

  a

  20

  b

  7

  +

  b

  15

  等于（　　）

  A． 9 4

  B． 37 8

  C． 79 14

  D． 149 24
  組卷：1459引用：57難度：0.9

  解析

• 2．已知函數

  f

  （

  x

  ）

  =

  4

  cos

  （

  ωx

  +

  π

  6

  ）

  sinωx

  +

  cos

  （

  π

  -

  2

  ωx

  ）

  ，其中ω＞0．若函數f（x）在

  [

  -

  π

  6

  ，

  5

  π

  6

  ]

  上為增函數，則ω的最大值為（　　）

  A． 3 10

  B． 1 2

  C． 3 2

  D．2
  組卷：51引用：1難度：0.6

  解析

• 3．長方體各面上的對角線所確定的平面個數是（　　）

  A．20

  B．14

  C．12

  D．6
  組卷：25引用：1難度：0.9

  解析

• 4．設集合A={x|x-2=0}，集合B={x|x²-4=0}，則A∩B等于（　　）

  A．{-2}

  B．{2}

  C．{-2，2}

  D．?
  組卷：1引用：3難度：0.8

  解析

• 5．焦點坐標為（-1，0）的拋物線的標準方程是（　　）

  A．y2=-2x

  B．x2=2y

  C．x2=-4y

  D．y2=-4x
  組卷：292引用：3難度：0.7

  解析

• 6．已知a=3^e（其中e為自然對數的底數），b=π³，c=3^π，則（　　）

  A．a＜b＜c

  B．b＜a＜c

  C．c＜a＜b

  D．a＜c＜b
  組卷：105引用：4難度：0.5

  解析

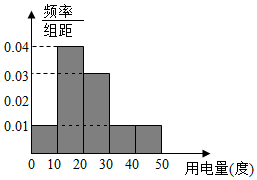• 7．供電部門對某社區1000位居民2017年12月份人均用電情況進行統計后，按人均用電量分為[0，10），[10，20），[20，30），[30，40），[40，50]五組，整理得到如下的頻率分布直方圖，則下列說法錯誤的是（　　）

  A．12月份人均用電量人數最多的一組有400人

  B．12月份人均用電量不低于20度的有500人

  C．12月份人均用電量為25度

  D．在這1000位居民中任選1位協助收費，選到的居民用電量在[30，40）一組的概率為 1 10
  組卷：776引用：10難度：0.7

  解析

• 8．已知復數z=

  1

  +

  i

  1

  -

  i

  ，以下結論正確的是（　　）

  A．z2022是純虛數

  B．|z+1|=2

  C．z? z =-1

  D．在復平面內，復數 z +z?i對應的點位于第三象限
  組卷：28引用：1難度：0.7

  解析

二、選擇題：本題共4小題，每小題5分，共20分.在每小題給出的選項中，有多項符合題目要求.全部選對的得5分，部分選對的得2分，有選錯的得0分.

• 9．《九章算術》中稱一個正方體內兩個互相垂直的內切圓柱所圍成的幾何體為“牟合方蓋”（如圖所示），已知該正方體ABCD-A₁B₁C₁D₁棱長為2，下列命題正確的是（　　）

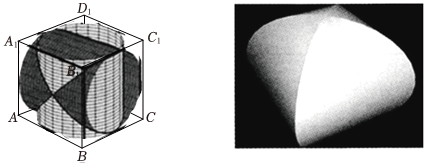
  A．正方體ABCD-A1B1C1D1的外接球中存在一條直徑被截面AC1D和截面ACB1三等分

  B．正方體ABCD-A1B1C1D1的內切球體積大于該牟合方蓋的內切球的體積

  C．正方體ABCD-A1B1C1D1的內切球被平面A1C1D截得的截面面積為 π 3

  D．以正方體的頂點A為球心，2為半徑的球在該正方體內部部分的體積與正方體ABCD-A1B1C1D1的棱切球的體積之比為 2 4
  組卷：108引用：2難度：0.6

  解析

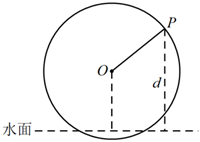• 10．如圖，一個半徑為3m的筒車按逆時針方向每分鐘轉1.5圈，筒車的軸心O距離水面的高度為2.2m.設筒車上的某個盛水筒P到水面的距離為d（單位：m）（在水面下則d為負數）．若以盛水筒P剛浮出水面時開始計算時間，d與時間t（單位：s）之間的關系為d=Asin（ωt+φ）+b（A＞0，ω＞0，-

  π

  2

  ＜φ＜

  π

  2

  ），則下列結論正確的是（　　）

  A．A=3

  B． ω = 4 π 3

  C． sinφ = - 11 15

  D．b=-0.8
  組卷：180引用：4難度：0.7

  解析

• 11．關于函數f（x）=

  1

  x

  -

  5

  x

  ，下列說法正確的是（　　）

  A．定義域為（0，+∞）	B．是偶函數
  C．在（0，+∞）上遞減	D．圖像關于原點對稱
  組卷：55引用：4難度：0.8

  解析

• 12．已知方程

  x

  2

  4

  -

  t

  +

  y

  2

  t

  -

  1

  =1表示的曲線為C．給出以下四個判斷，其中正確的是（　　）

  A．當1＜t＜4時，曲線C表示橢圓

  B．當t＞4或t＜1時，曲線C表示雙曲線

  C．若曲線C表示焦點在x軸上的橢圓，則1＜t＜ 5 2

  D．若曲線C表示焦點在y軸上的雙曲線，則t＞4
  組卷：608引用：29難度：0.7

  解析

三、填空題：本題共4小題，每小題5分，共20分.

• 13．（x+y）（x-y）⁷的展開式中x⁶y²的系數是

  ．
  組卷：120引用：4難度：0.7

  解析

• 14．在△ABC中，O為其內部一點，且滿足

  OA

  +

  OB

  +4

  OC

  =

  0

  ，則△ABC和△AOC的面積比是

  ．
  組卷：14引用：1難度：0.5

  解析

• 15．曲邊梯形由曲線y=x²+1，y=0，x=1，x=2所圍成，過曲線y=x²+1，x∈[1，2]上一點P作切線，使得此切線從曲邊梯形上切出一個面積最大的普通梯形，則此普通梯形的最大面積為

  ．
  組卷：35引用：2難度：0.5

  解析
• 16．系統找不到該試題

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

• 17．2023上海蒸蒸日上迎新跑于2023年2月19日舉辦，該賽事設有21.6公里競速跑、5.4公里歡樂跑兩個項目．某馬拉松興趣小組為慶祝該賽事，舉行一場小組內有關于馬拉松知識的有獎比賽，一共有25人報名（包括20位新成員和5位老成員），其中20位新成員的得分情況如表所示（滿分30分）：
  

  得分	[0，5）	[5，10）	[10，15）	[15，20）	[20，25）	[25，30]
  人數	2	3	4	6	4	1

  得分在20分以上（含20分）的成員獲得獎品一份．
  （1）請根據上述表格中的統計數據，將下面的2×2列聯表補充完全，并通過計算判斷在20位新成員中，是否有90%的把握認為“獲獎”與性別有關？
  

  	沒獲獎	獲獎	合計
  男		4
  女	7		8
  合計

  （2）若5名老成員的性別相同并全部獲獎，且進行計算發現在所有參賽人員中，有90%的把握認為“獲獎”與性別有關．請判斷這5名老成員的性別？
  附：參考公式：

  K

  2

  =

  n

  （

  ad

  -

  bc

  ）

  2

  （

  a

  +

  b

  ）

  （

  c

  +

  d

  ）

  （

  a

  +

  c

  ）

  （

  b

  +

  d

  ）

  ，

  n

  =

  a

  +

  b

  +

  c

  +

  d

  ．
  臨界值表：
  

  P（K2＞k）	0.100	0.050	0.010	0.001
  k	2.706	3.841	6.635	10.828
  組卷：98引用：4難度：0.5

  解析

• 18．已知拋物線Γ：y²=4x的焦點為F，準線為l.
  （1）若F為雙曲線C：

  2

  x

  2

  -

  y

  2

  b

  2

  =

  1

  （b＞0）的一個焦點，求雙曲線C的漸近線方程；
  （2）設l與x軸的交點為E，點P在第一象限，且在Γ上，若

  |

  PE

  |

  |

  PF

  |

  =

  2

  ，求直線EP的方程；
  （3）經過點F且斜率為k（k≠0）的直線l₁與Γ相交于A、B兩點，O為坐標原點，直線OA、OB分別與l相交于點M、N．試探究：以線段MN為直徑的圓C是否過定點，若是，求出定點的坐標；若不是，說明理由．
  組卷：83引用：1難度：0.3

  解析

• 19．在等差數列{a_n}中，S_n為其前n項和（n∈N₊）．若a₂=3，S₄=16．
  （1）求數列{a_n}的通項公式；
  （2）設

  b

  n

  =

  1

  a

  n

  ?

  a

  n

  +

  1

  ，求數列{b_n}的前n項和T_n．
  組卷：165引用：5難度：0.6

  解析

• 20．已知關于x的方程x²-2kx+k²-k-1=0有兩個不相等的實數根x₁，x₂．
  （1）若k=5，求

  x

  1

  x

  2

  2

  +

  x

  2

  1

  x

  2

  的值；
  （2）若x₁-3x₂=2，求實數k的值．
  組卷：61引用：2難度：0.5

  解析

• 21．在四棱錐P-ABCD中，底面ABCD為直角梯形，AD∥BC，AD⊥AB，側面PAB⊥底面ABCD，PA=PB=AD=

  1

  2

  BC=2，且E，F分別為PC，CD的中點．
  （1）證明：DE∥平面PAB；
  （2）若直線PF與平面PAB所成的角為60°，求平面PAB與平面PCD所成銳二面角的余弦值．
  組卷：289引用：26難度：0.6

  解析

• 22．在①△ABC面積S_△ABC=2，②∠ADC=

  π

  6

  這兩個條件中任選一個，補充在下面問題中，求AC．如圖，在平面四邊形ABCD中，∠ABC=

  3

  π

  4

  ，∠BAC=∠DAC，______，CD=2AB=4，求AC．
  組卷：410引用：8難度：0.7

  解析