當前位置：試卷中心 > 試卷詳情

2021-2022學年河南省新鄉市輝縣第一高級中學高二（上）第一次段考數學試卷（理科）

發布：2025/6/29 14:0:13

一、選擇題（本大題共12小題，每小題5分，共60分。在每小題給出的四個選項中，只有一項是符合題目要求的）

1．若x,y滿足約束條件
2
x
-
y
-
1
≤
0
，
x
+
2
≥
0
，
y
-
2
≤
0
，
，則z=x+y的最大值為（　　）
A．-7 B．0 C．
7
2
D．7
組卷：12引用：3難度：0.6
解析
2．對于非零實數a,b,“
1
a
＞
1
b
”成立的一個充分而不必要條件是（　　）
A．a³＜b³ B．|a-b|=|a|+|b|
C．log₂a＜0＜log_b2 D．ab（a-b）＜0
組卷：51引用：1難度：0.8
解析
3．若（a+b+c）（b+c-a）=3bc,且ccosB=bcosC，那么△ABC是（　　）
A．等邊三角形 B．等腰三角形
C．直角三角形 D．等腰直角三角形
組卷：59引用：3難度：0.8
解析
4．已知數列{a_n}滿足a_n+1=2a_n（n≥1）且a₂=-1，則a₈=（　　）
A．64 B．
-
1
64
C．-64 D．
1
64
組卷：31引用：2難度：0.8
解析
5．一小孩玩拋硬幣跳格子游戲，規則如下：拋一枚硬幣，若正面朝上，往前跳兩格，若反面朝上，往前跳一格．記跳到第n格可能有a_n種情況，{a_n}的前n項和為S_n，則S₈=（　　）
A．56 B．68 C．87 D．95
組卷：68引用：2難度：0.7
解析
6．已知{a_n}為遞增等差數列，等比數列{b_n}以a₁，a₂為前兩項且公比為3，若b₅=a_m，則m=（　　）
A．13 B．41 C．57 D．86
組卷：82引用：3難度：0.7
解析

7．下列命題中正確的是（　　）

A．命題p：“?x₀∈R，

＜

”，則命題￢p：?x∈R，x²-2x+1＞0

B．“lna＞lnb”是“2^a＞2^b”的充要條件

C．命題p：?x₀∈R，tan x₀=2；命題q：對?x∈R，總有2^x＞0；則p∧q是真命題

D．命題“若x²=2，則

或

”的逆否命題是“若

≠

或

≠

，則x²≠2”

組卷：31引用：1難度：0.7

解析

8．若a＞0，b＞0，a+b=2，則
a
+
b
ab
的最小值為（　　）
A．
2
2
B．
2
C．1 D．2
組卷：457引用：1難度：0.6
解析
9．在△ABC中，若a=7，b=8，
cos
B
=
1
7
，則∠A的大小為（　　）
A．
π
6
B．
π
3
C．
5
π
6
D．
π
3
或
2
π
3
組卷：486引用：4難度：0.7
解析
10．北京2022年冬奧會開幕式用“一朵雪花”的故事連接中國與世界，傳遞了“人類命運共同體”的理念．“雪花曲線”也叫“科赫雪花”，它是由等邊三角形三邊生成的科赫曲線組成的，是一種分形幾何．圖1是長度為1的線段，將圖1中的線段三等分，以中間部分的線段為邊，向外作等邊三角形，再將中間部分的線段去掉得到圖2，這稱為“一次分形”；用同樣的方法把圖2中的每條線段重復上述操作，得到圖3，這稱為“二次分形”；…．依次進行“n次分形”（n∈N^*）．規定：一個分形圖中所有線段的長度之和為該分形圖的長度．若要得到一個長度不小于40的分形圖，則n的最小值是（　　）（參考數據：lg3≈0.477，lg2≈0.301）
A．11 B．12 C．13 D．14
組卷：41引用：5難度：0.7
解析
11．在△ABC中，角A，B，C的對邊分別為a,b,c,若
asin
A
+
C
2
=
bsin
A
，則角B=（　　）
A．
π
6
或
5
π
6
B．
π
3
或
2
π
3
C．
π
6
D．
π
3
組卷：257引用：1難度：0.6
解析
12．在△ABC中，已知A=60°，
a
=
6
，b=4，那么滿足條件的△ABC（　　）
A．有0個解 B．有1個解 C．有2個 D．不能確定
組卷：12引用：2難度：0.9
解析

二、填空題（每小題5分，共20分，把答案填在答題卷中橫線上）

13．已知不等式4x²-12x+b＞0的解集為
{
x
|
x
≠
3
2
，
x
∈
R
}
，則b值為
．
組卷：43引用：2難度：0.7
解析
14．在△ABC中，角A，B，C所對的邊分別為a,b,c.若
sin
A
=
cos
（
π
2
-
B
）
，a=3，c=2，則cosC=

；△ABC的面積為

．
組卷：237引用：2難度：0.5
解析
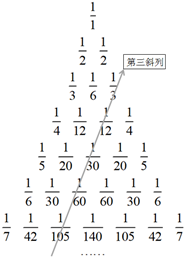15．將楊輝三角中的每一個數
C
r
n
都換成
1
（
n
+
1
）
C
r
n
，得到一個如圖所示的分數三角形，稱為萊布尼茨三角形．記第三斜列構成數列{a_n}，即
a
1
=
1
3
，
a
2
=
1
12
，
a
3
=
1
30
，…
，則{a_n}的前n項和S_n=
．
組卷：46引用：1難度：0.6
解析
16．如圖，目標函數z=ax-y的可行域為四邊形OACB（含邊界），若（
2
3
，
4
5
）是該目標函數z=ax-y的最優解，則a的取值范圍是
．
組卷：12引用：3難度：0.7
解析

三、解答題（本大題6小題，共70分。解答應寫出文字說明，證明過程或演算步驟）

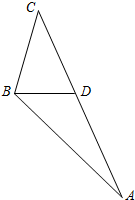17．近日我漁船編隊在釣魚島附近點A周圍海域作業，在B處的海監15船測得A在其南偏東45°方向上，測得漁政船310在其北偏東15°方向上，且與B的距離為4
3
海里的C處．某時刻，海監15船發現日本船向在點A周圍海域作業的我漁船編隊靠近，上級指示漁政船310立刻全速前往點A周圍海域執法，海監15船原地監測．漁政船310走到B正東方向D處時，測得距離B為4
2
海里．若漁政船以23海里/小時的速度航行，求其到達點A所需的時間．
組卷：23引用：2難度：0.5
解析
18．設函數f（x）=x²+mx+n,已知不等式f（x）＜0的解集為{x|1＜x＜4}．
（1）求m和n的值；
（2）若f（x）≥ax對任意x＞0恒成立，求a的取值范圍．
組卷：434引用：3難度：0.7
解析
19．新冠肺炎疫情發生以后，口罩供不應求，某口罩廠日夜加班生產，生產口罩的固定成本為400萬元，每生產x萬箱（x＞0，x∈N），需另投入成本p（x）萬元．當產量不足60萬箱時，
p
（
x
）
=
1
2
x
2
+
50
x
；當產量不小于60萬箱時，
p
（
x
）
=
101
x
+
6400
x
-
1860
，若每箱口罩售價100元，通過市場分析，該口罩廠生產的口罩可以全部銷售完．
（1）求口罩銷售利潤y（萬元）關于產量x（萬箱）的函數關系式；
（2）當產量為多少萬箱時，該口罩生產廠在生產中所獲利潤最大？
組卷：69引用：1難度：0.6
解析
20．已知等差數列{a_n}的前n項和為S_n，且滿足a₄+a₆=18，S₁₁=121．
（1）求數列{a_n}的通項公式；
（2）設b_n=（a_n+3）2ⁿ，數列{b_n}的前n項和為T_n，求T_n．
組卷：686引用：10難度：0.5
解析
21．在三角形ABC中，已知
tan
B
=
1
2
，
cos
C
=
-
10
10
．
（1）求角A的值；
（2）若△ABC的面積為
3
10
，求邊BC的長．
組卷：238引用：2難度：0.5
解析
22．在等差數列{a_n}中，a₂=5，a₄+a₇=24．
（1）求{a_n}的通項公式；
（2）求數列
{
1
a
n
a
n
+
1
}
的前n項和S_n．
組卷：27引用：2難度：0.7
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．a³＜b³	B．\|a-b\|=\|a\|+\|b\|
C．log₂a＜0＜log_b2	D．ab（a-b）＜0

A．等邊三角形	B．等腰三角形
C．直角三角形	D．等腰直角三角形

2021-2022學年河南省新鄉市輝縣第一高級中學高二（上）第一次段考數學試卷（理科）

一、選擇題（本大題共12小題，每小題5分，共60分。在每小題給出的四個選項中，只有一項是符合題目要求的）

1．若x,y滿足約束條件2x-y-1≤0，x+2≥0，y-2≤0，，則z=x+y的最大值為（ ）

2．對于非零實數a,b,“1a＞1b”成立的一個充分而不必要條件是（ ）

3．若（a+b+c）（b+c-a）=3bc,且ccosB=bcosC，那么△ABC是（ ）

4．已知數列{an}滿足an+1=2an（n≥1）且a2=-1，則a8=（ ）

5．一小孩玩拋硬幣跳格子游戲，規則如下：拋一枚硬幣，若正面朝上，往前跳兩格，若反面朝上，往前跳一格．記跳到第n格可能有an種情況，{an}的前n項和為Sn，則S8=（ ）

6．已知{an}為遞增等差數列，等比數列{bn}以a1，a2為前兩項且公比為3，若b5=am，則m=（ ）

7．下列命題中正確的是（ ）

8．若a＞0，b＞0，a+b=2，則a+bab的最小值為（ ）

9．在△ABC中，若a=7，b=8，cosB=17，則∠A的大小為（ ）

11．在△ABC中，角A，B，C的對邊分別為a,b,c,若asinA+C2=bsinA，則角B=（ ）

12．在△ABC中，已知A=60°，a=6，b=4，那么滿足條件的△ABC（ ）

二、填空題（每小題5分，共20分，把答案填在答題卷中橫線上）

13．已知不等式4x2-12x+b＞0的解集為{x|x≠32，x∈R}，則b值為 ．

14．在△ABC中，角A，B，C所對的邊分別為a,b,c.若sinA=cos（π2-B），a=3，c=2，則cosC= ；△ABC的面積為 ．

15．將楊輝三角中的每一個數Crn都換成1（n+1）Crn，得到一個如圖所示的分數三角形，稱為萊布尼茨三角形．記第三斜列構成數列{an}，即a1=13，a2=112，a3=130，…，則{an}的前n項和Sn=．

16．如圖，目標函數z=ax-y的可行域為四邊形OACB（含邊界），若（23，45）是該目標函數z=ax-y的最優解，則a的取值范圍是．

三、解答題（本大題6小題，共70分。解答應寫出文字說明，證明過程或演算步驟）

18．設函數f（x）=x2+mx+n,已知不等式f（x）＜0的解集為{x|1＜x＜4}．（1）求m和n的值；（2）若f（x）≥ax對任意x＞0恒成立，求a的取值范圍．

20．已知等差數列{an}的前n項和為Sn，且滿足a4+a6=18，S11=121．（1）求數列{an}的通項公式；（2）設bn=（an+3）2n，數列{bn}的前n項和為Tn，求Tn．

21．在三角形ABC中，已知tanB=12，cosC=-1010．（1）求角A的值；（2）若△ABC的面積為310，求邊BC的長．

22．在等差數列{an}中，a2=5，a4+a7=24．（1）求{an}的通項公式；（2）求數列{1anan+1}的前n項和Sn．

1．若x,y滿足約束條件
2
x
-
y
-
1
≤
0
，
x
+
2
≥
0
，
y
-
2
≤
0
，
，則z=x+y的最大值為（　　）

2．對于非零實數a,b,“
1
a
＞
1
b
”成立的一個充分而不必要條件是（　　）

3．若（a+b+c）（b+c-a）=3bc,且ccosB=bcosC，那么△ABC是（　　）

4．已知數列{a_n}滿足a_n+1=2a_n（n≥1）且a₂=-1，則a₈=（　　）

5．一小孩玩拋硬幣跳格子游戲，規則如下：拋一枚硬幣，若正面朝上，往前跳兩格，若反面朝上，往前跳一格．記跳到第n格可能有a_n種情況，{a_n}的前n項和為S_n，則S₈=（　　）

6．已知{a_n}為遞增等差數列，等比數列{b_n}以a₁，a₂為前兩項且公比為3，若b₅=a_m，則m=（　　）

7．下列命題中正確的是（　　）

8．若a＞0，b＞0，a+b=2，則
a
+
b
ab
的最小值為（　　）

9．在△ABC中，若a=7，b=8，
cos
B
=
1
7
，則∠A的大小為（　　）

11．在△ABC中，角A，B，C的對邊分別為a,b,c,若
asin
A
+
C
2
=
bsin
A
，則角B=（　　）

12．在△ABC中，已知A=60°，
a
=
6
，b=4，那么滿足條件的△ABC（　　）

13．已知不等式4x²-12x+b＞0的解集為
{
x
|
x
≠
3
2
，
x
∈
R
}
，則b值為
．

14．在△ABC中，角A，B，C所對的邊分別為a,b,c.若
sin
A
=
cos
（
π
2
-
B
）
，a=3，c=2，則cosC=

；△ABC的面積為

．

15．將楊輝三角中的每一個數
C
r
n
都換成
1
（
n
+
1
）
C
r
n
，得到一個如圖所示的分數三角形，稱為萊布尼茨三角形．記第三斜列構成數列{a_n}，即
a
1
=
1
3
，
a
2
=
1
12
，
a
3
=
1
30
，…
，則{a_n}的前n項和S_n=
．

16．如圖，目標函數z=ax-y的可行域為四邊形OACB（含邊界），若（
2
3
，
4
5
）是該目標函數z=ax-y的最優解，則a的取值范圍是
．

18．設函數f（x）=x²+mx+n,已知不等式f（x）＜0的解集為{x|1＜x＜4}．
（1）求m和n的值；
（2）若f（x）≥ax對任意x＞0恒成立，求a的取值范圍．

20．已知等差數列{a_n}的前n項和為S_n，且滿足a₄+a₆=18，S₁₁=121．
（1）求數列{a_n}的通項公式；
（2）設b_n=（a_n+3）2ⁿ，數列{b_n}的前n項和為T_n，求T_n．

21．在三角形ABC中，已知
tan
B
=
1
2
，
cos
C
=
-
10
10
．
（1）求角A的值；
（2）若△ABC的面積為
3
10
，求邊BC的長．

22．在等差數列{a_n}中，a₂=5，a₄+a₇=24．
（1）求{a_n}的通項公式；
（2）求數列
{
1
a
n
a
n
+
1
}
的前n項和S_n．