2021年西南名校聯(lián)盟高考數(shù)學(xué)聯(lián)考試卷（理科）

一、選擇題：本大題共12小題，每小題5分，共60分.在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的.

• 1．如果用1N的力能將彈簧拉長(zhǎng)1cm,為了將彈簧拉長(zhǎng)6cm,所耗費(fèi)的功為（　　）

  A．0.18J

  B．0.26J

  C．0.12J

  D．0.28J
  組卷：0引用：1難度：0.7

  解析

• 2．若

  （

  1

  x

  +

  x

  2

  3

  ）

  n

  （

  n

  ∈

  N

  *

  ）

  的展開(kāi)式中存在常數(shù)項(xiàng)，則n=（　　）

  A．2k（k∈N*）

  B．3k（k∈N*）

  C．5k（k∈N*）

  D．7k（k∈N*）
  組卷：25引用：2難度：0.7

  解析

• 3．命題p：ax²+2x+1=0有實(shí)數(shù)根，若￢p是假命題，則實(shí)數(shù)a的取值范圍是（　　）

  A．{a|a＜1}

  B．{a|a≤1}

  C．{a|a＞1}

  D．{a|a≥1}
  組卷：534引用：8難度：0.6

  解析

• 4．“∠A和∠B是對(duì)頂角”是“∠A=∠B”的（　　）

  A．充分條件	B．必要條件
  C．充要條件	D．既不充分也不必要條件
  組卷：5引用：1難度：0.7

  解析

• 5．“∠A和∠B是對(duì)頂角”是“∠A=∠B”的（　　）

  A．充分條件	B．必要條件
  C．充要條件	D．既不充分也不必要條件
  組卷：4引用：1難度：0.9

  解析

• 6．為計(jì)算S=1+2³+3²+4³+5²+…+99²+100³設(shè)計(jì)了如圖所示的程序框圖，則在和兩個(gè)空白框中分別可以填入（　　）

  A．i≤101和N=N+（i+1）3	B．i＜99和N=N+（i+1）2
  C．i≤99和N=N+（i+1）2	D．i＜101和N=N+（i+1）3
  組卷：58引用：2難度：0.7

  解析

• 7．已知集合A={x|2≤2^x≤4}，B=（0，4），則A∪B=（　　）

  A．（1，4）

  B．（0，4）

  C．（0，2]

  D．[1，2]
  組卷：55引用：1難度：0.9

  解析

• 8．設(shè)函數(shù)y=sinx的定義域?yàn)閇a,b]，值域?yàn)閇-

  1

  2

  ，1]，給出以下四個(gè)結(jié)論：
  ①b-a的最小值為

  2

  π

  3

  
  ②b-a的最大值為

  4

  π

  3

  
  ③a可能等于2kπ-

  π

  6

  （k∈z）     
  ④b可能等于2kπ-

  π

  6

  （k∈z）
  其中正確的有（　　）

  A．4個(gè)

  B．3個(gè)

  C．2個(gè)

  D．1個(gè)
  組卷：68引用：2難度：0.9

  解析

• 9．復(fù)數(shù)z滿足1+zi+zi²=|1-

  3

  i|，則z=（　　）

  A．1+i

  B． 1 2 + 1 2 i

  C．- 1 2 - 1 2 i

  D．- 1 2 + 1 2 i
  組卷：132引用：3難度：0.8

  解析

• 10．如圖所示的三角形數(shù)陣由一個(gè)等差數(shù)列2，5，8，11，14…排成，按照此規(guī)律，數(shù)陣中第21行從左至右的第6個(gè)數(shù)是（　　）

  A．632

  B．644

  C．647

  D．650
  組卷：36引用：1難度：0.8

  解析

• 11．判斷e³，3^e，e^π，π^e，3^π，π³中最大的數(shù)為（　　）

  A．eπ

  B．πe

  C．π3

  D．3π
  組卷：4引用：3難度：0.5

  解析

• 12．已知雙曲線

  Γ

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的左、右焦點(diǎn)分別為F₁，F(xiàn)₂，P是圓x²+y²=c²（

  c

  =

  a

  2

  +

  b

  2

  ）與Γ的一個(gè)交點(diǎn)，若△PF₁F₂的內(nèi)切圓的半徑為a,則Γ的離心率為（　　）

  A． 3 + 1

  B． 2 + 1

  C．2

  D． 3 2
  組卷：198引用：6難度：0.5

  解析

二、填空題：本大題共4小題，每小題5分，共20分.把答案填在答題卡中的橫線上.

• 13．已知拋物線C：y²=6x,過(guò)P（3，2）的直線l交拋物線C于A，B兩點(diǎn)，且|PA|=|PB|，則直線l的方程為

  ．
  組卷：161引用：12難度：0.7

  解析

• 14．在△ABC中，已知AB=2，AC=4，∠BAC=60°，M為線段BC的中點(diǎn)，N為線段AC上一動(dòng)點(diǎn)，則

  MN

  ?

  BN

  的最小值為

  ．
  組卷：75引用：4難度：0.5

  解析

• 15．已知在正四面體ABCD中，點(diǎn)E在棱AC上，F(xiàn)為棱AD的中點(diǎn)．若BE+EF的最小值為

  42

  ，則該四面體外接球的表面積是

  ．
  組卷：91引用：3難度：0.5

  解析

• 16．不等式組

  4 x + 3 y ＜ 12

  x - y ＜ - 1

  y ≥ 0

  x ≥ 0

  表示的平面區(qū)域內(nèi)的整點(diǎn)的個(gè)數(shù)是

  個(gè)．
  組卷：39引用：1難度：0.7

  解析

三、解答題：本大題共5小題，共70分.解答應(yīng)寫(xiě)出必要的文字說(shuō)明、證明過(guò)程或演算步驟.17～21題為必考題，每個(gè)試題考生都必須作答.第22、23題為選考題，考生根據(jù)要求作答.（一）必考題：共60分.

• 17．在三角形ABC中，內(nèi)角A，B，C的對(duì)邊分別為a,b,c,a=2b,且

  2

  csin

  B

  =

  acos

  （

  C

  -

  π

  6

  ）

  ．
  （1）求角C；
  （2）E為三角形ABC所在平面內(nèi)的一點(diǎn)，

  AE

  =

  AB

  +

  AC

  且

  |

  AE

  |

  =

  2

  ，求線段CE的長(zhǎng)．
  組卷：142引用：4難度：0.6

  解析

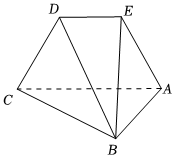• 18．如圖，在多面體ABCDE中，平面ABC⊥平面ACDE，四邊形ACDE是等腰梯形，ED∥AC，AB⊥AC，

  AE

  =

  ED

  =

  DC

  =

  1

  2

  AC

  =

  1

  ．
  （1）若AB=1，求BD與平面ACDE所成角的正弦值；
  （2）若平面BDE與平面BCD的夾角為

  π

  4

  ，求AB的長(zhǎng)．
  組卷：189引用：1難度：0.6

  解析

• 19．已知函數(shù)

  f

  （

  x

  ）

  =

  ln

  （

  2

  x

  +

  a

  ）

  （

  a

  ∈

  R

  ）

  ．
  （1）若函數(shù)F（x）=f（x）-ln[（2-a）x+3a-3]有唯一零點(diǎn)，求實(shí)數(shù)a的取值范圍；
  （2）若對(duì)任意實(shí)數(shù)

  m

  ∈

  [

  3

  4

  ，

  1

  ]

  ，對(duì)任意x₁，x₂∈[m,4m-1]，恒有|f（x₁）-f（x₂）|≤ln2成立，求正實(shí)數(shù)a的取值范圍．
  組卷：218引用：5難度：0.3

  解析

• 20．已知橢圓C中心在坐標(biāo)原點(diǎn)，焦點(diǎn)坐標(biāo)為（2，0），短軸長(zhǎng)為

  4

  3

  ．
  （1）求橢圓C的標(biāo)準(zhǔn)方程及離心率，并寫(xiě)出橢圓的準(zhǔn)線方程；
  （2）設(shè)P是橢圓C上一點(diǎn)，且點(diǎn)P與橢圓C的兩個(gè)焦點(diǎn)F₁，F(xiàn)₂構(gòu)成一個(gè)直角三角形，且PF₁＞PF₂，求

  P

  F

  1

  P

  F

  2

  的值．
  組卷：36引用：1難度：0.1

  解析

• 21．在平面直角坐標(biāo)系xOy中，曲線C₁的參數(shù)方程為

  x = 3 + 2 2 cosα ，

  y = 2 2 sinα

  （α為參數(shù)）．以坐標(biāo)原點(diǎn)O為極點(diǎn)，x軸的正半軸為極軸建立極坐標(biāo)系，曲線C₂的極坐標(biāo)方程為ρsin²θ-6cosθ=0．
  （1）求曲線C₁的普通方程與曲線C₂的直角坐標(biāo)方程；
  （2）設(shè)直線l：

  x = 3 + 1 2 t

  y = 3 2 t

  （t為參數(shù)）與曲線C₂，C₁的交點(diǎn)從上到下依次為P，M，N，Q，求|PM|+|NQ|的值．
  組卷：108引用：5難度：0.6

  解析

[選修4-4：坐標(biāo)系與參數(shù)方程]

• 22．旅游承載著人們對(duì)美好生活的向往．隨著近些年人們收入和消費(fèi)水平不斷提高，對(duì)品質(zhì)生活的需求也日益升級(jí)，旅游市場(chǎng)開(kāi)啟了快速增長(zhǎng)的時(shí)代．某旅游景區(qū)為吸引旅客，提供了A，B兩條路線方案．該景區(qū)為進(jìn)一步了解旅客對(duì)這兩條路線的選擇情況和滿意度評(píng)價(jià)（“好”或“一般”），對(duì)300名旅客的路線選擇和評(píng)價(jià)進(jìn)行了統(tǒng)計(jì)，如表：

  	A路線		B路線		合計(jì)
  	好	一般	好	一般
  男	10	20	55	35	120
  女	90	30	20	40	180
  合計(jì)	100	50	75	75	300

  （1）根據(jù)以上數(shù)據(jù)，在犯錯(cuò)誤的概率不超過(guò)0.1%的前提下，可以認(rèn)為對(duì)A，B兩條路線的選擇與性別有關(guān)嗎？
  （2）某人計(jì)劃到該景區(qū)旅游，預(yù)先在網(wǎng)上了解了對(duì)這兩條路線的評(píng)價(jià)，假設(shè)他分別看了兩條路線各三條評(píng)價(jià)（評(píng)價(jià)“好”或“一般”的可能性以前面統(tǒng)計(jì)的占比為參考），若評(píng)價(jià)為“好”的計(jì)5分，評(píng)價(jià)為“一般”的計(jì)2分，以期望值作為參考，那么你認(rèn)為這個(gè)人會(huì)選擇哪一條路線？請(qǐng)用計(jì)算說(shuō)明理由．
  附：

  χ

  2

  =

  n

  （

  ad

  -

  bc

  ）

  2

  （

  a

  +

  b

  ）

  （

  c

  +

  d

  ）

  （

  a

  +

  c

  ）

  （

  b

  +

  d

  ）

  ，其中n=a+b+c+d.
  

  α=P（χ2≥k）	0.05	0.01	0.001
  k	3.841	6.635	10.828
  組卷：36引用：1難度：0.6

  解析

[選修4-5：不等式選講]

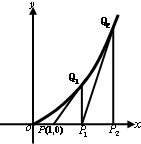• 23．如圖，過(guò)點(diǎn)P（1，0）作曲線C：y=x²（x∈（0，+∞））的切線，切點(diǎn)為Q₁，設(shè)點(diǎn)Q₁在x軸上的投影是點(diǎn)P₁；又過(guò)點(diǎn)P₁作曲線C的切線，切點(diǎn)為Q₂，設(shè)Q₂在x軸上的投影是P₂；…；依此下去，得到一系列點(diǎn)Q₁，Q₂，Q₃-Q_n，設(shè)點(diǎn)Q_n的橫坐標(biāo)為a_n．
  （1）求直線PQ₁的方程；
  （2）求數(shù)列{a_n}的通項(xiàng)公式；
  （3）記Q_n到直線P_nQ_n+1的距離為d_n，求證：n≥2時(shí)，

  1

  d

  1

  +

  1

  d

  2

  +…

  1

  d

  n

  ＞3．
  組卷：37引用：3難度：0.3

  解析