2024-2025學年四川省達州市流江實驗學校八年級（下）月考數(shù)學試卷（6月份）
發(fā)布：2025/6/27 15:0:8
一、選擇題（本大題共10小題，總分40分）
-
1．已知△ABC的三邊分別是a、b、c,下列條件中不能判斷△ABC為直角三角形的是（ ）
組卷：780引用：5難度：0.7 -
2．在平行四邊形ABCD中，∠A：∠B：∠C：∠D的值可能是（ ）
組卷：900引用：22難度：0.7 -
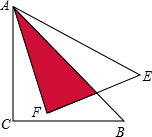3．如圖，將等腰直角三角形ABC繞點A逆時針旋轉(zhuǎn)15度得到△AEF，若AC=，則陰影部分的面積為（ ）3組卷：1682引用：13難度：0.7 -
4．如果a＞b,那么下列不等式中正確的是（ ）
組卷：389引用：10難度：0.7 -
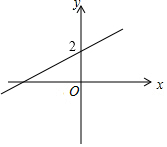5．如圖，一次函數(shù)y=kx+b（k＞0）的圖象過點（0，2），則不等式kx+b-2＞0的解集是（ ）組卷：2507引用：9難度：0.6 -
6．若a、b、c是實數(shù)，a≠0，ax3+bx2-c的一個因式是x2+2x-1，則
等于（ ）ba組卷：321引用：2難度：0.7 -
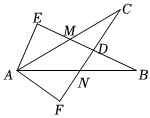7．如圖，∠E=∠F=90°，∠B=∠C，AE=AF，結(jié)論①EM=FN，②CD=DN，③∠FAN=∠EAM，④△ACN≌△ABM中，正確的有（ ）組卷：2374引用：11難度：0.7 -
8．下列所述圖形中，是軸對稱圖形但不是中心對稱圖形的是（ ）
組卷：1415引用：21難度：0.9 -
9．甲、乙二人從鄭州出發(fā)到西安，甲乘坐高鐵，乙乘坐普通列車，結(jié)果甲比乙少用5h.已知高鐵的平均速度比普通列車快180km/h,求高鐵、普通列車的平均速度分別是多少．假設(shè)從鄭州到西安的高鐵、普通列車線路長均為520km,高鐵的平均速度為x km/h,則根據(jù)題意可列方程為（ ）
組卷：665引用：4難度：0.6 -
10．已知，正多邊形的一個外角是30°，則這個正多邊形是（ ）
組卷：447引用：4難度：0.9
二、填空題（本大題共5小題，總分20分）
-
11．在△ABC中，∠ABC=90°，∠A=30°，如果AB=3cm,那么BC=．
組卷：5引用：1難度：0.7 -
12．將△ABC繞點C順時針旋轉(zhuǎn)35°，得到△A'B'C'，A'B'交AC于點D，交AB于點E，∠AEB′=°．組卷：47引用：2難度：0.6 -
13．直接寫出因式分解的結(jié)果：（1）x2y2-y2=
（2）a2-6a+9=．組卷：45引用：1難度：0.7 -
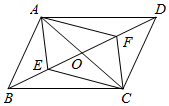14．如圖，在?ABCD中，AC，BD相交于點O，點E，F(xiàn)在對角線BD上，有下列條件：①BF=DE；②AE=CF；③∠EAB=∠FCD；④AF∥CE．其中一定能判定四邊形AECF是平行四邊形的是 ．組卷：1425引用：4難度：0.5 -
15．已知關(guān)于x的分式方程
=mx-4有增根，則m=．6+x4-x組卷：412引用：4難度：0.9
三、解答題（本大題共10小題，總分90分）
-
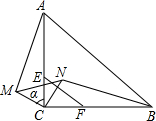16．如圖，已知，在△ABC中，CA=CB，∠ACB=90°，E，F(xiàn)分別是CA，CB邊的三等分點，將△ECF繞點C逆時針旋轉(zhuǎn)α角（0°＜α＜90°），得到△MCN，連接AM，BN．
（1）求證：AM=BN；
（2）當MA∥CN時，試求旋轉(zhuǎn)角α的余弦值．組卷：2474引用：59難度：0.5 -
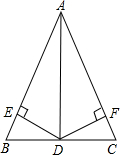17．如圖，在△ABC中，AB=AC，D是BC的中點，DE⊥AB于點E，DF⊥AC于點F．
（1）求證：DE=DF；
（2）如果S△ABC=14，AC=7，求DE的長．組卷：1020引用：8難度：0.1 -
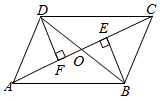18．如圖，在?ABCD中，O是對角線AC、BD的交點．BE⊥AC，DF⊥AC，垂足分別為點E、F．
（1）求證：OE=OF．
（2）若?ABCD的面積為80．AC=16，OF=2，求tan∠OBE的值．組卷：76引用：2難度：0.6 -
19．化簡：
÷3-xx-2．（5x-2-x-2）組卷：113引用：4難度：0.3 -
20．計算題：
（1）解不等式3（x-1）＜5x+2，并在數(shù)軸上表示解集；
（2）解不等式組，并在數(shù)軸上表示解集；x+4≤612（x-3）＞-2
（3）解方程：；xx-1-3x+1=1
（4）解方程：3x2-6x-2=0．組卷：79引用：2難度：0.5 -
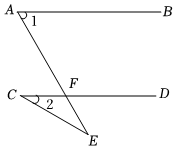21．如圖，直線AB∥CD，若∠1=60°，∠2=30°，求證：△FCE是等腰三角形．組卷：758引用：6難度：0.8 -
22．閱讀下面材料，在代數(shù)式中，我們把一個二次多項式化為一個完全平方式與一個常數(shù)的和的方法叫做配方法．配方法是一種重要的解決問題的數(shù)學方法，它不僅可以將一個看似不能分解的多項式因式分解，還能求代數(shù)式最大值，最小值等問題．
例如：求代數(shù)式：x2-12x+2020的最小值．
解：原式=x2-12x+62-62+2020
=（x-6）2+1984
∵（x-6）2≥0，
∴當x=6時，（x-6）2的值最小，最小值為0，
∴（x-6）2+1984≥1984，
∴當（x-6）2=0時，（x-6）2+1984的值最小，最小值為1984，
∴代數(shù)式：x2-12x+2020的最小值是1984．
例如：分解因式：x2-120x+3456
解：原式=x2-2×60x+602-602+3456
=（x-60）2-144
=（x-60）2-122
=（x-60+12）（x-60-12）
=（x-48）（x-72）．
（1）分解因式x2-46x+520；
（2）若y=-x2+2x+1313，求y的最大值；
（3）當m,n為何值時，代數(shù)式m2-2mn-2m+2n2-4n+2030有最小值，并求出這個最小值．組卷：1326引用：3難度：0.5 -
23．一輛汽車開往距離出發(fā)地180km的目的地，出發(fā)后第一小時內(nèi)按原計劃的速度勻速行駛，一小時后以原來速度的1.5倍勻速行駛，并比原計劃提前40min到達目的地，設(shè)前一小時行駛的速度為xkm/h.
（1）直接用x的式子表示提速后走完剩余路程的時間為 h.
（2）求汽車實際走完全程所花的時間；
（3）若汽車按原路返回，司機準備一半路程以mkm/h的速度行駛，另一半路程以nkm/h的速度行駛（m≠n），朋友提醒他一半時間以mkm/h的速度行駛，另一半時間以nkm/h的速度行駛更快，你覺得誰的方案更快？請說明理由．組卷：1128引用：7難度：0.7 -
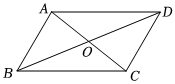24．已知：如圖，平行四邊形ABCD的對角線AC、BD相交于點O．
求證：OA=OC，OB=OD．
證明：∵四邊形ABCD是平行四邊形，
∴AD=，AD∥，
∴∠OAD=，∠ODA=，
∴△AOD≌（ASA），
∴OA=，OB=．組卷：10引用：1難度：0.6 -
25．如圖所示，三角形ABC是等邊三角形，以A為旋轉(zhuǎn)中心，畫出三角形AMB（α＜60°）按逆時針方向旋轉(zhuǎn)至AB與AC重合．組卷：2引用：1難度：0.6