2025年山東省濟(jì)寧市中考數(shù)學(xué)試卷
發(fā)布：2025/6/27 15:0:7
一、選擇題：本題共10小題，每小題3分，共30分。每小題只有一個(gè)選項(xiàng)符合題目要求。
-
1．數(shù)軸上點(diǎn)A到原點(diǎn)的距離為2，點(diǎn)B到點(diǎn)A的距離為3，則點(diǎn)B表示的所有數(shù)的積為（ ）
組卷：134引用：3難度：0.7 -
2．某機(jī)構(gòu)對(duì)30萬(wàn)人的調(diào)查顯示，沉迷于手機(jī)上網(wǎng)的初中生大約占7%，則這部分沉迷于手機(jī)上網(wǎng)的初中生人數(shù)，可用科學(xué)記數(shù)法表示為（ ）
組卷：157引用：57難度：0.9 -
3．某賓館共有80間客房．賓館負(fù)責(zé)人根據(jù)經(jīng)驗(yàn)作出預(yù)測(cè)：今年7月份，每天的房間空閑數(shù)y（間）與定價(jià)x（元/間）之間滿(mǎn)足y=
x-42（x≥168）．若賓館每天的日常運(yùn)營(yíng)成本為5000元，有客人入住的房間，賓館每天每間另外還需支出28元的各種費(fèi)用，賓館想要獲得最大利潤(rùn)，同時(shí)也想讓客人得到實(shí)惠，應(yīng)將房間定價(jià)確定為（ ）14組卷：2215引用：8難度：0.6 -
4．已知ab≠0，下列計(jì)算正確的是（ ）
組卷：71引用：1難度：0.5 -
5．書(shū)架上有3本小說(shuō)、2本散文，從中隨機(jī)抽取2本都是小說(shuō)的概率是（ ）
組卷：1380引用：65難度：0.7 -
6．如圖，正五邊形ABCDE內(nèi)接于⊙O，其半徑為1，作OF⊥BC交⊙O于點(diǎn)F，則圖中影部分的面積為（ ）組卷：53引用：1難度：0.5 -
7．《孫子算經(jīng)》是中國(guó)古代重要的數(shù)學(xué)著作，成書(shū)大約在一千五百年前．其中一道題，原文是：“今三人共車(chē)，兩車(chē)空；二人共車(chē)，九人步．問(wèn)人與車(chē)各幾何？”意思是：現(xiàn)有若干人和車(chē)，若每輛車(chē)乘坐3人，則空余兩輛車(chē)；若每輛車(chē)乘坐2人，則有9人步行．問(wèn)人與車(chē)各多少？設(shè)有x人，y輛車(chē)，可列方程組為（ ）
組卷：1637引用：35難度：0.7 -
8．如圖，A、B是雙曲線(xiàn)y=上的兩點(diǎn)，經(jīng)過(guò)A、B兩點(diǎn)分別作AC∥y軸，BC∥x軸，兩線(xiàn)交于點(diǎn)C，已知S△AOC=3，S△ABC=9，則k的值為（ ）kx組卷：263引用：2難度：0.6 -
9．如圖四個(gè)幾何體中，同一個(gè)幾何體的左視圖與俯視圖相同的幾何體共有（ ）
組卷：112引用：66難度：0.9 -
10．下列四個(gè)圖案中，既是軸對(duì)稱(chēng)圖形又是中心對(duì)稱(chēng)圖形的圖案是（ ）
組卷：130引用：11難度：0.9
二、填空題：本題共5小題，每小題3分，共15分。
-
11．如果一個(gè)正比例函數(shù)的圖象與反比例函數(shù)y=
的圖象交于A(yíng)（x1，y1），B（x2，y2）兩點(diǎn)，那么（x2-x1）（y2-y1）的值為6x．組卷：2168引用：56難度：0.7 -
12．平行四邊形ABCD，若∠A-∠B=30°，則∠C=
，∠D=．組卷：50引用：7難度：0.9 -
13．將點(diǎn)A先向上平移3個(gè)單位，再向左平移2個(gè)單位，得到點(diǎn)B（-1，1），則點(diǎn)A的坐標(biāo)是 ．
組卷：142引用：4難度：0.7 -
14．要使分式
有意義，x的取值應(yīng)滿(mǎn)足．2x-3x+4組卷：158引用：2難度：0.8 -
15．關(guān)于x的一元二次方程2x2+3x+m=0有兩個(gè)相等的實(shí)數(shù)根，則m的值為 ．
組卷：54引用：3難度：0.5
三、解答題：本題共8小題，共75分.解答應(yīng)寫(xiě)出文字說(shuō)明、證明過(guò)程或演算步驟
-
16．如圖，拋物線(xiàn)y=ax2+bx+c經(jīng)過(guò)點(diǎn)A（-3，0），B（1，0），C（0，-3）．
（1）求拋物線(xiàn)的解析式；
（2）若點(diǎn)P為第三象限內(nèi)拋物線(xiàn)上的一點(diǎn)，設(shè)△PAC的面積為S，求S的最大值并求出此時(shí)點(diǎn)P的坐標(biāo)；
（3）設(shè)拋物線(xiàn)的頂點(diǎn)為D，DE⊥x軸于點(diǎn)E，在y軸上是否存在點(diǎn)M，使得△ADM是直角三角形？若存在，請(qǐng)直接寫(xiě)出點(diǎn)M的坐標(biāo)；若不存在，請(qǐng)說(shuō)明理由．組卷：2071引用：63難度：0.5 -
17．如圖1，矩形ABCD中，AB=15，BC=20，將矩形ABCD繞著點(diǎn)A順時(shí)針旋轉(zhuǎn)，得到矩形BEFG．
（1）當(dāng)點(diǎn)E落在BD上時(shí)，則線(xiàn)段DE的長(zhǎng)度等于 ；
（2）如圖2，當(dāng)點(diǎn)E落在A(yíng)C上時(shí)，求△BCE的面積；
（3）如圖3，連接AE、CE、AG、CG，判斷線(xiàn)段AE與CG的位置關(guān)系且說(shuō)明理由，并求CE2+AG2的值；
（4）在旋轉(zhuǎn)過(guò)程中，請(qǐng)直接寫(xiě)出S△BCE+S△ABG的最大值．組卷：378引用：3難度：0.2 -
18．如圖1，一輛汽車(chē)的背面，有一種特殊形狀的刮雨器，忽略刮雨器的寬度可抽象為一條折線(xiàn)OAB，如圖2所示，量得連桿OA長(zhǎng)為10cm,雨刮桿AB長(zhǎng)為48cm,∠OAB=120°．若啟動(dòng)一次刮雨器，雨刮桿AB正好掃到水平線(xiàn)CD的位置，如圖3所示．
（1）求雨刮桿AB旋轉(zhuǎn)的最大角度及O、B兩點(diǎn)之間的距離；（結(jié)果精確到0.01）
（2）求雨刮桿AB掃過(guò)的最大面積．（結(jié)果保留π的整數(shù)倍）（參考數(shù)據(jù)：sin60°=，cos60°=32，tan60°=12，3≈26.851，可使用科學(xué)計(jì)算器）721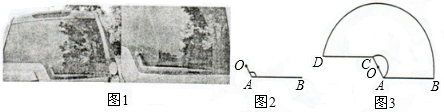
組卷：673引用：56難度：0.5 -
19．如圖，四邊形OABC是平行四邊形，以O(shè)為圓心，OA為半徑的圓交AB于點(diǎn)D，延長(zhǎng)AO交⊙O于點(diǎn)E，連接CD，CE，若CE是⊙O的切線(xiàn)，解答下列問(wèn)題：
（1）求證：CD是⊙O的切線(xiàn)；
（2）若BC=3，CD=4，求平行四邊形OABC的面積．組卷：1446引用：63難度：0.5 -
20．先化簡(jiǎn)，再求值：
，其中a=3．（a2a-2-1a-2）÷a2-2a+1a-2組卷：196引用：56難度：0.7 -
21．某校為了解七、八年級(jí)學(xué)生對(duì)“防溺水”安全知識(shí)的掌握情況，從七、八年級(jí)各隨機(jī)抽取50名學(xué)生進(jìn)行測(cè)試，并對(duì)成績(jī)（百分制并取整數(shù)）進(jìn)行整理、描述和分析，部分信息如圖：
a.七年級(jí)成績(jī)頻數(shù)分布直方圖：
b.七年級(jí)成績(jī)?cè)?0≤x＜80這一組的是：
70 72 74 75 76 76 77 77 77 78 79
c.七、八年級(jí)成績(jī)的平均數(shù)、中位數(shù)如下：
根據(jù)以上信息，回答下列問(wèn)題．年級(jí) 平均數(shù) 中位數(shù) 七 76.9 m 八 79.2 79.5
（1）在這次測(cè)試中，七年級(jí)在80分以上（含80分）的有人；
（2）表中m的值為；
（3）在這次測(cè)試中，七年級(jí)學(xué)生甲與八年級(jí)學(xué)生乙的成績(jī)都是78分，則兩位學(xué)生在各自年級(jí)的排名中（填甲或乙）更靠前；
（4）該校七年級(jí)學(xué)生有400人，假設(shè)全部參加此次測(cè)試，請(qǐng)估算七年級(jí)成績(jī)超過(guò)平均數(shù)76.9分的人數(shù)．組卷：96引用：2難度：0.5 -
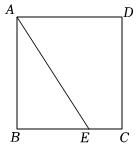22．如圖，在正方形ABCD中，點(diǎn)E在BC上，連接AE．
（1）用尺規(guī)完成以下基本作圖：過(guò)點(diǎn)D作AE的垂線(xiàn)，分別與AB、AE交于點(diǎn)F、G；（不寫(xiě)作法和證明，保留作圖痕跡）
（2）在（1）所作的圖形中，求證：AE=DF．（請(qǐng)補(bǔ)全下面的證明過(guò)程）
證明：∵四邊形ABCD是正方形，
∴∠ABC=∠BAD=90°，AB=AD．
∵∠BAD=90°，
∴∠BAE+∠DAE=90°．
∵DF⊥AE，
∴∠AGD=．
∴+∠DAE=90°．
又∵∠BAE+∠DAE=90°，
∴．
在△ABE和△DAF中：（），∠ABE=∠DAF（??）∠BAE=∠ADF
∴△ABE≌△DAF（ASA）．
∴AE=DF．組卷：130引用：2難度：0.9 -
23．新農(nóng)村社區(qū)改造中，有一部分樓盤(pán)要對(duì)外銷(xiāo)售，某樓盤(pán)共23層，銷(xiāo)售價(jià)格如下：第八層樓房售價(jià)為4000元/米2，從第八層起每上升一層，每平方米的售價(jià)提高50元；反之，樓層每下降一層，每平方米的售價(jià)降低30元，已知該樓盤(pán)每套樓房面積均為120米2．
若購(gòu)買(mǎi)者一次性付清所有房款，開(kāi)發(fā)商有兩種優(yōu)惠方案：
方案一：降價(jià)8%，另外每套樓房贈(zèng)送a元裝修基金；
方案二：降價(jià)10%，沒(méi)有其他贈(zèng)送．
（1）請(qǐng)寫(xiě)出售價(jià)y（元/米2）與樓層x（1≤x≤23，x取整數(shù)）之間的函數(shù)關(guān)系式；
（2）老王要購(gòu)買(mǎi)第十六層的一套樓房，若他一次性付清購(gòu)房款，請(qǐng)幫他計(jì)算哪種優(yōu)惠方案更加合算．組卷：4228引用：77難度：0.5