2024-2025學年山東省臨沂市蒙陰三中八年級（下）月考數學試卷（6月份）

一、選擇題（本題共10小題，每小題3分，共30分，每小題只有一個選項符合題目要求）

• 1．函數y=

  x

  +

  2

  中，自變量x的取值范圍是（　　）

  A．x＞-2

  B．x≥-2

  C．x≠2

  D．x≤-2
  組卷：668引用：96難度：0.9

  解析

• 2．滿足

  -

  2

  ＜x＜

  5

  的整數x的個數（　　）

  A．2個

  B．3個

  C．4個

  D．5個
  組卷：100引用：5難度：0.7

  解析

• 3．如圖，菱形ABCD的對角線AC、BD相交于點O，∠ABD=30°，BC=4，則邊AD與BC之間的距離為（　　）

  A．2 5

  B．2 3

  C． 5

  D． 3
  組卷：1251引用：9難度：0.7

  解析

• 4．將直線y=

  1

  2

  x-1向下平移3個單位長度得到直線l,則直線l的解析式為（　　）

  A． y = 1 2 x - 4

  B． y = 1 2 x - 3

  C． y = 1 2 x + 2

  D． y = - 1 2 x - 3
  組卷：374引用：1難度：0.7

  解析

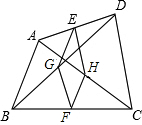• 5．如圖，已知點E、F分別是四邊形ABCD的邊AD、BC的中點，G、H分別是對角線BD、AC的中點，要使四邊形EGFH是菱形，則四邊形ABCD需滿足的條件是（　　）

  A．AB=CD

  B．AC=BD

  C．AC⊥BD

  D．AD=BC
  組卷：2554引用：13難度：0.7

  解析

• 6．下列四個命題：①直徑是弦；②經過三個點一定可以作圓；③三角形的內心到三角形各邊的距離都相等；④相等的弦所對的弧相等．其中正確的有（　　）

  A．4個

  B．3個

  C．2個

  D．1個
  組卷：311引用：7難度：0.9

  解析

• 7．一次函數y₁=kx+b（k≠0，k、b是常數）與y₂=mx+3（m≠0，m是常數）的圖象交于點D（1，2），下列結論正確的序號是（　　）
  ①關于x的方程kx+b=mx+3的解為x=1；②一次函數y₂=mx+3（m≠0）圖象上任意不同兩點A（x_a，y_a）和B（x_b，y_b）滿足：（x_a-x_b）（y_a-y_b）＜0；③若|y₁-y₂|=b-3（b＞3），則x=0；④若b＜3，且b≠2，則當x＞1時，y₁＞y₂．

  A．②③④

  B．①②④

  C．①②③

  D．①②③④
  組卷：697引用：2難度：0.5

  解析

• 8．如圖，在?ABCD中，O是對角線AC與BD的交點，AB⊥AC，若AB=8，AC=12，則BD的長是（　　）

  A．20

  B．22

  C．24

  D．26
  組卷：185引用：4難度：0.5

  解析

• 9．如圖所示，BE⊥AC于點D，且AD=CD，BD=ED，若∠ABC=54°，則∠E=（　　）

  A．25°

  B．27°

  C．30°

  D．45°
  組卷：1316引用：51難度：0.9

  解析

• 10．下列條件中，不能判定一個四邊形是平行四邊形的是（　　）

  A．兩組對邊分別平行

  B．一組對邊平行且相等

  C．一組對邊相等且一組對角相等

  D．兩組對角分別相等
  組卷：378引用：6難度：0.9

  解析

二、填空題（本題共6小題，每小題3分，共18分）

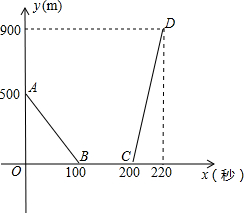• 11．設甲、乙兩車在同一直線公路上勻速行駛，開始甲車在乙車的前面，當乙車追上甲車后，兩車停下來，把乙車的貨物轉給甲車，然后甲車繼續前行，乙車向原地返回．設x秒后兩車間的距離為y米，y關于x的函數關系如圖所示，則甲車的速度是

  米/秒．
  組卷：1913引用：74難度：0.7

  解析

• 12．已知x=2-

  3

  ，則代數式

  x

  2

  +

  （

  2

  +

  3

  ）

  x

  的值是

  ．
  組卷：423引用：10難度：0.8

  解析

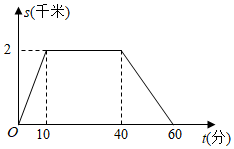• 13．星期天，小蓮上午8：00從家里出發到圖書館去借書，再回到家．她離家的距離s（千米）與時間t（分）的關系如圖所示，則上午8：45小蓮離家的距離是

  千米．
  組卷：256引用：7難度：0.6

  解析

• 14．點（-

  1

  2

  ，m）和點（2，n）在直線y=2x+b上，則m與n的大小關系是

  ．
  組卷：1535引用：17難度：0.6

  解析

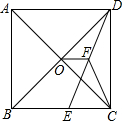• 15．如圖，在正方形ABCD中，對角線AC與BD相交于點O，E為BC上一點，CE=5，F為DE的中點．若△CEF的周長為18，則OF的長為

  ．
  組卷：5404引用：64難度：0.7

  解析

• 16．若一次函數y=2x+2的圖象經過點（3，m），則m=

  ．
  組卷：890引用：8難度：0.6

  解析

三、解答題（本題共7小題，共72分，解答應寫出文字說明、證明過程或演算步驟）

• 17．某工廠有甲種原料69千克，乙種原料52千克，現計劃用這兩種原料生產A，B兩種型號的產品共80件，已知每件A型號產品需要甲種原料0.6千克，乙種原料0.9千克；每件B型號產品需要甲種原料1.1千克，乙種原料0.4千克．請解答下列問題：
  （1）該工廠有哪幾種生產方案？
  （2）在這批產品全部售出的條件下，若1件A型號產品獲利35元，1件B型號產品獲利25元，（1）中哪種方案獲利最大？最大利潤是多少？
  （3）在（2）的條件下，工廠決定將所獲利潤的25%全部用于再次購進甲、乙兩種原料，要求每種原料至少購進4千克，且購進每種原料的數量均為整數．若甲種原料每千克40元，乙種原料每千克60元，請直接寫出購買甲、乙兩種原料之和最多的方案．
  組卷：1195引用：57難度：0.3

  解析

• 18．化簡：

  3

  3

  -（

  3

  -1）²+（π+

  3

  ）⁰-

  27

  +|

  3

  -2|．
  組卷：77引用：1難度：0.3

  解析

• 19．建立模型：
  如圖1，等腰Rt△ABC中，∠ABC=90°，CB=BA，直線ED經過點B，過A作AD⊥ED于D，過C作CE⊥ED于E．則易證△ADB≌△BEC．這個模型我們稱之為“一線三垂直”．它可以把傾斜的線段AB和直角∠ABC轉化為橫平豎直的線段和直角，所以在平面直角坐標系中被大量使用．
  模型應用：
  （1）如圖2，點A（0，4），點B（3，0），△ABC是等腰直角三角形．
  ①若∠ABC=90°，且點C在第一象限，求點C的坐標；
  ②若AB為直角邊，求點C的坐標；
  （2）如圖3，長方形MFNO，O為坐標原點，F的坐標為（8，6），M、N分別在坐標軸上，P是線段NF上動點，設PN=n,已知點G在第一象限，且是直線y=2x一6上的一點，若△MPG是以G為直角頂點的等腰直角三角形，請直接寫出點G的坐標．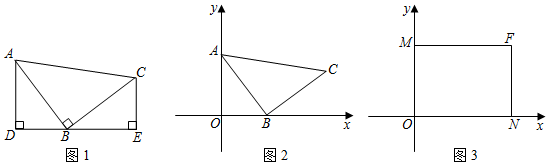
  
  組卷：1794引用：4難度：0.2

  解析

• 20．我們定義：若一個四邊形的一條對角線把四邊形分成兩個等腰三角形，則稱這條對角線叫這個四邊形的和諧線，這個四邊形叫做和諧四邊形．如正方形就是和諧四邊形．
  如圖，等腰Rt△ABD中，∠BAD=90°．若點C為平面上一點，AC為凸四邊形ABCD的和諧線，且AB=BC，請直接寫出∠ABC的度數．
  組卷：41引用：1難度：0.6

  解析

• 21．在正方形ABCD中，AB=4，O為對角線AC、BD的交點．
  （1）如圖1，延長OC，使CE=OC，作正方形OEFG，使點G落在OD的延長線上，連接DE、AG．求證：DE=AG；
  （2）如圖2，將問題（1）中的正方形OEFG繞點O逆時針旋轉α（0＜α＜180°），得到正方形OE′F′G′，連接AE′、E′G′．
  ①當α=30°時，求點A到E′G′的距離；
  ②在旋轉過程中，求△AE′G′面積的最小值，并求此時的旋轉角α．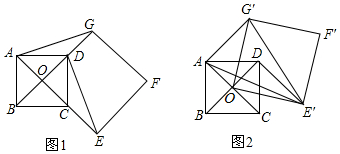
  
  組卷：540引用：3難度：0.2

  解析

• 22．如圖，某小區一健身中心的平面圖，活動區時面積為200m²的長方形，休息區是直角三角形，請你設計一下半圓區餐飲區的面積．
  
  組卷：82引用：2難度：0.5

  解析

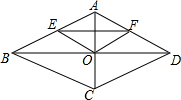• 23．如圖，菱形ABCD的對角線AC，BD相交于點O，點E，F分別是邊AB，AD的中點．
  （1）請判斷△OEF的形狀，并證明你的結論；
  （2）若AB=13，AC=10，請求出線段EF的長．
  組卷：3221引用：69難度：0.5

  解析