2025年廣東省東莞外國語學校中考數學二模試卷

一、選擇題（本大題共10小題，每小題3分，共30分．在每小題給出的四個選項中，只有一個選項是符合題目要求的）

• 1．在一次數學測試中，第5小組同學的分數（單位：分）分別是：85、63、101、85、85、101、72，則這組數據的眾數是（　　）

  A．63

  B．72

  C．85

  D．101
  組卷：137引用：2難度：0.8

  解析

• 2．若拋物線y=-x²+bx+c經過點（-2，3），則2c-4b-9的值是（　　）

  A．5

  B．-1

  C．4

  D．18
  組卷：2952引用：19難度：0.9

  解析

• 3．如圖，A（-2，3）、B（3，2）是平面直角坐標系中的兩點，在x軸上有一點C能使AC與BC的長度之和最小，則點C的坐標為（　　）

  A．（-2，0）

  B．（-1，0）

  C．（1，0）

  D．（0，0）
  組卷：301引用：1難度：0.6

  解析

• 4．某停車場入口的欄桿如圖所示，欄桿從水平位置AB繞點O旋轉到CD的位置．已知AO=4米，若欄桿的旋轉角∠AOD=27°，則欄桿端點A升高的高度為（　　）

  A． 4 sin 27 ° 米

  B．4sin27°米

  C．4cos27°米

  D．4tan27°米
  組卷：152引用：4難度：0.5

  解析

• 5．下列圖形中，既是軸對稱圖形又是中心對稱圖形的是（　　）

  A．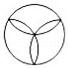

  B．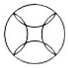

  C．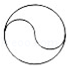

  D．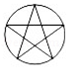
  組卷：8引用：1難度：0.9

  解析

• 6．已知a=2⁶⁶，b=3⁵⁵，c=4⁴⁴，那么a、b、c的大小關系是（　　）

  A．a＞b＞c

  B．b＞c＞a

  C．a＜b＜c

  D．c＞a＞b
  組卷：56引用：3難度：0.9

  解析

• 7．在四邊形ABCD中，∠A=∠B=∠C，點E在邊AB上，∠AED=60°，則一定有（　　）

  A．∠ADE=20°	B．∠ADE=30°
  C．∠ADE= 1 2 ∠ADC	D．∠ADE= 1 3 ∠ADC
  組卷：4238引用：71難度：0.7

  解析

• 8．教練記錄了甲、乙兩名運動員在一次1500米長跑比賽中的成績，他們的速度v（單位：米/秒）與路程s（單位：米）的關系如圖所示，下列說法錯誤的是（　　）

  A．最后50米乙的速度比甲快

  B．前500米乙一直跑在甲的前面

  C．第500米的時候甲追上了乙

  D．第500米至第1450米階段甲的用時比乙短
  組卷：106引用：1難度：0.7

  解析

• 9．如圖，直線a∥b,直線a與b分別和直線c相交，若∠1=70°，則∠2的度數是（　　）

  A．70°

  B．90°

  C．100°

  D．110°
  組卷：27引用：1難度：0.7

  解析

• 10．n為正整數，x=2ⁿ+2ⁿ⁺¹，y=2ⁿ⁺²+2ⁿ⁺³，則（　　）

  A．y=2x

  B．y=3x

  C．y=4x

  D．y=6x
  組卷：39引用：3難度：0.7

  解析

二、填空題（本大題共5個小題，每小題3分，共15分）

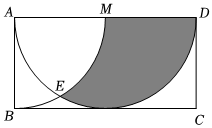• 11．矩形ABCD中，AB=2，以A為圓心，AB為半徑作圓弧交于AD點M，且M為邊AD的中點，以AD為直徑的圓交弧BM于點E，則陰影部分面積

  ．
  組卷：317引用：3難度：0.6

  解析

• 12．某校決定從兩名男生和三名女生中選出兩名同學作為蘭州國際馬拉松賽的志愿者，則選出一男一女的概率是

  ．
  組卷：201引用：63難度：0.9

  解析

• 13．某年級有學生246人，其中男生比女生人數的2倍少3人，問男女學生各多少人？設女生人數為x人，男生人數為y人，可列方程組為

   

  ．
  組卷：353引用：13難度：0.9

  解析

• 14．如果x₁，x₂是方程x²-5x+6=0的兩個根，那么x₁?x₂=

  ．
  組卷：82引用：23難度：0.7

  解析

• 15．分解因式：m²-10m=

   

  ．
  組卷：186引用：61難度：0.9

  解析

三、解答題（一）（本大題共3小題，每小題7分，共21分）

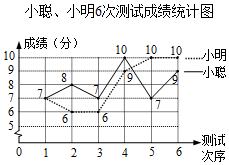• 16．小聰、小明準備代表班級參加學校“黨史知識”競賽，班主任對這兩名同學測試了6次，獲得如圖測試成績折線統計圖．根據圖中信息，解答下列問題：
  （1）要評價每位同學成績的平均水平，你選擇什么統計量？求這個統計量．
  （2）求小聰成績的方差．
  （3）現求得小明成績的方差為S_小明²=3（單位：平方分）．根據折線統計圖及上面兩小題的計算，你認為哪位同學的成績較好？請簡述理由．
  組卷：587引用：15難度：0.7

  解析

• 17．在△ABC和△ADE中，∠BAC=∠ADE=90°，AB=AC，DE=DA．且AC＞AD．
  （1）如圖1，點D在線段AC上時，連接BE，若AC=4

  2

  ，AE=6，求線段EB的長；
  （2）如圖2，將圖1中△ADE繞著點A逆時針旋轉，使點D在△ABC的內部，連接BD，CD．線段AE，BD相交于點F，過點A作AH⊥BC交BC于點H，當∠DCB=∠DAC時，求證：BF=DF；
  （3）如圖3，點C'是點C關于AB的對稱點，連接C′A，C′B．在（2）的基礎上繼續逆時針旋轉△ADE，過B作AD的平行線，交直線EA于點G．連接C′G，CG，BD．若BC=4，當線段C′G最短時，直接寫出△ACG的面積．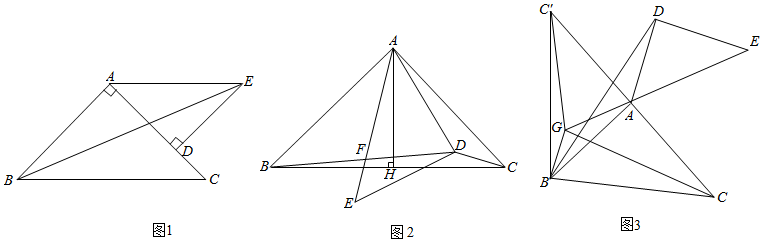
  
  組卷：389引用：1難度：0.2

  解析

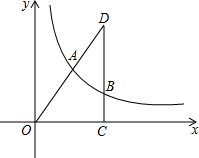• 18．已知：如圖，在平面直角坐標系中，Rt△OCD的一邊OC在x軸上，∠C=90°，點D在第一象限，OC=3，DC=4，反比例函數的圖象經過OD的中點A．
  （1）求該反比例函數的解析式；
  （2）若該反比例函數y=

  k

  x

  （k≠0）的圖象與Rt△OCD的另一邊DC交于點B，求過A、B兩點的直線的解析式；
  （3）在反比例函數y=

  k

  x

  （k≠0）第一象限的圖象上，是否存在點E，使得四邊形ACED為梯形？若存在，求出E的坐標；若不存在，說明理由．
  組卷：72引用：1難度：0.5

  解析

四、解答題（二）（本大題共3小題，每小題9分，共27分）

• 19．先化簡，再求值；

  （

  1

  +

  1

  a

  -

  3

  ）

  ÷

  a

  2

  -

  4

  a

  -

  3

  ，其中

  a

  =

  3

  -

  2

  ．
  組卷：173引用：6難度：0.7

  解析

• 20．已知拋物線y=-x²+bx+c的對稱軸為直線x=1，其圖象與x軸相交于A，B兩點，與y軸相交于點C（0，3）．
  （1）求b,c的值；
  （2）直線l與x軸相交于點P．
  ①如圖1，若l∥y軸，且與線段AC及拋物線分別相交于點E，F，點C關于直線x=1的對稱點為點D，求四邊形CEDF面積的最大值；
  ②如圖2，若直線l與線段BC相交于點Q，當△PCQ∽△CAP時，求直線l的表達式．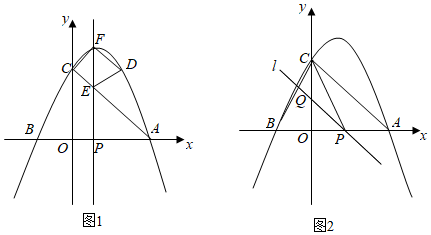
  
  組卷：2058引用：4難度：0.3

  解析

• 21．某學校2021年在某商場購買甲、乙兩種不同足球，購買甲種足球共花費2500元，購買乙種足球共花費1800元，購買甲種足球數量是購買乙種足球數量的2倍．且購買一個乙種足球比購買一個甲種足球多花22元．
  （1）求購買一個甲種足球、一個乙種足球各需多少元？
  （2）2022年這所學校決定再次購買甲、乙兩種足球共50個．恰逢該商場對兩種足球的售價進行調整，甲種足球售價比第一次購買時提高了12%，乙種足球售價比第一次購買時降低了5%．如果此次購買甲、乙兩種足球的總費用不超過3050元，那么這所學校最多可購買多少個乙種足球？
  組卷：302引用：4難度：0.5

  解析

五、解答題（三）（本大題共2小題，第22題13分，第23題14分，共27分）

• 22．計算：

  4

  +|-2|+（-6）×（-

  2

  3

  ）．
  組卷：567引用：51難度：0.7

  解析

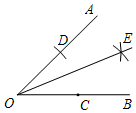• 23．如圖是小西設計的“作已知角∠AOB的平分線”的尺規作圖過程：
  ①在射線OB上取一點C；
  ②以點O為圓心，OC長為半徑作弧，交射線OA于點D；
  ③分別以點C，D為圓心，OC長為半徑作弧，兩弧相交于點E；
  ④作射線OE．
  則射線OE即為∠AOB的角平分線．
  請觀察圖形回答下列問題：
  （1）由步驟②知，線段OC，OD的數量關系是

  ；連接DE，CE，線段CO，CE的數量關系是

  ；
  （2）在（1）的條件下，若∠EOC=25°，求∠ECB的度數．
  組卷：262引用：2難度：0.5

  解析