當前位置：試卷中心 > 試卷詳情

2025年山東省青島市中考數學模擬試卷（七）

發布：2025/6/27 16:0:8

一、選擇題（本大題共9小題，每小題3分，共27分）

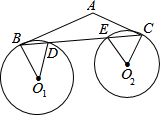1．如圖，AB切圓O₁于B點，AC切圓O₂于C點，BC分別交圓O₁、圓O₂于D、E兩點．若∠BO₁D=40°，∠CO₂E=60°，則∠A的度數為何？（　　）
A．100 B．120 C．130 D．140
組卷：633引用：58難度：0.9
解析
2．用科學記數法表示0.0000907，得（　　）
A．9.07×10^-4 B．9.07×10^-5 C．9.07×10^-6 D．9.07×10^-7
組卷：653引用：33難度：0.9
解析
3．若實數x、y、z滿足（x-z）²-4（x-y）（y-z）=0，則下列式子一定成立的是（　　）
A．x+y+z=0 B．x+y-2z=0 C．y+z-2x=0 D．z+x-2y=0
組卷：1453引用：27難度：0.9
解析
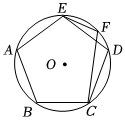4．如圖，正五邊形ABCDE內接于圓O，點F是
?
EC
上一點，則∠EFC的大小為（　　）
A．120° B．105° C．108° D．150°
組卷：27引用：1難度：0.6
解析
5．下列圖形中，既是軸對稱圖形又是中心對稱圖形的是（　　）
A．正三角形 B．平行四邊形 C．矩形 D．正五邊形
組卷：244引用：59難度：0.9
解析
6．當a＜0時，2，2+a,2-a,a中最大的是（　　）
A．2 B．2+a C．2-a D．a
組卷：48引用：2難度：0.7
解析
7．如圖，在平面直角坐標系中，△AOB為等腰直角三角形∠OAB=90°，邊OA在x軸正半軸上OA=2，點B在第一象限內，將△AOB繞點O順時針旋轉，每次旋轉45°則第2023次旋轉后，點B的坐標為（　　）
A．
（
2
2
.
0
）
B．（2，2） C．
（
0
，
2
2
）
D．（2，-2）
組卷：206引用：2難度：0.4
解析
8．二次函數y=（x-1）²-2，若y隨x的增大而增大，則x的取值范圍是（　　）
A．x＞1 B．x＜1 C．x＞-1 D．x＜-1
組卷：426引用：4難度：0.6
解析
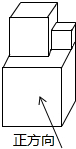9．如圖是三個大小不等的正方體拼成的幾何體，其中兩個較小正方體的棱長之和等于大正方體的棱長．該幾何體的主視圖、俯視圖和左視圖的面積分別是S₁，S₂，S₃，則S₁，S₂，S₃的大小關系是（　　）
A．S₁＞S₂＞S₃ B．S₃＞S₂＞S₁ C．S₂＞S₃＞S₁ D．S₁＞S₃＞S₂
組卷：1603引用：76難度：0.5
解析

二、填空題（本大題共6小題，每小題3分，共18分）

10．計算：cos²45°+
cos
30
°
2
sin
60
°
+
1
-
3
?tan30°=

．
組卷：5引用：1難度：0.7
解析
11．據市房管局統計，今年某周我市8個縣區的普通住宅成交量如下表：
區縣贛榆東海灌云灌南新浦海州連云港開發區
成交量（套） 105 101 53 72 110 50 56 88
則該周普通住宅成交量的中位數為

套．
組卷：65引用：46難度：0.7
解析
12．爸爸，媽媽，小慧、小弟，這四人今年的年齡之和是99歲，爸爸比媽媽大4歲，小慧比小弟大3歲，9年前，他們的年齡之和為65歲，由以上條件可知今年爸爸
歲．
組卷：108引用：2難度：0.5
解析
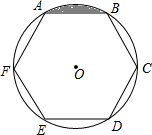13．如圖，六邊形ABCDEF為⊙O的內接正六邊形，若⊙O的半徑為2
3
，則陰影部分的面積為

．
組卷：851引用：59難度：0.5
解析
14．如圖，在矩形ABCD中，AB=6cm,BC=8cm,若將矩形折疊，使點B與點D重合，則折痕EF的長為
cm.
組卷：218引用：9難度：0.5
解析
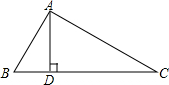15．如圖，△ABC中，∠BAC=90°，AD⊥BC于D，若AB=4，BD=2，則BC=
．
組卷：282引用：6難度：0.7
解析

三、作圖題（本大題滿分4分）

16．2013年4月20日，四川雅安發生里氏7.0級地震，救援隊救援時，利用生命探測儀在某建筑物廢墟下方探測到點C處有生命跡象，已知廢墟一側地面上兩探測點A、B相距4米，探測線與地面的夾角分別為30°和60°，如圖所示，試確定生命所在點C的深度（結果精確到0.1米，參考數據
2
≈1.41，
3
≈1.73）
組卷：588引用：59難度：0.5
解析

四、解答題（本大題共9小題，共71分）

17．七年級數學研究學習小組在某十字路口隨機調查部分市民對“社會主義核心價值觀”的了解情況，統計結果后繪制了如圖的兩幅不完整的統計圖，請結合圖中相關數據回答下列問題：

得分

A 50＜n≤60

B 60＜n≤70

C 70＜n≤80

D 80＜n≤90

E 90＜n≤100

（1）本次調查的總人數為
人，在扇形統計圖中“D”所在扇形的圓心角的度數為
；
（2）補全頻數分布圖；
（3）若在這一周里，該路口共有12000人通過，請估計得分超過80的大約有多少人？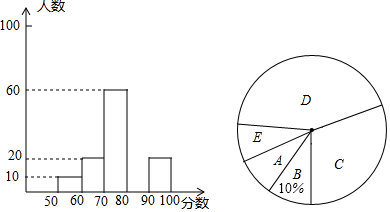

組卷：22引用：2難度：0.6

解析

18．如圖，矩形OABC的邊OA、OC分別在x軸、y軸的正半軸上，且OA=3，OC=2，將矩形OABC向上平移4個單位得到矩形O₁A₁B₁C₁．
（1）若反比例函數y=
k
1
x
和y=
k
2
x
的圖象分別經過點B、B₁，求k₁和k₂的值；
（2）將矩形O₁A₁B₁C₁向左平移得到O₂A₂B₂C₂，當點O₂、B₂在反比例函數y=
k
3
x
的圖象上時，求平移的距離和k₃的值．
組卷：2061引用：58難度：0.3
解析
19．已知△ABC是等邊三角形，四邊形ADEF是菱形，∠ADE=120°（AD＞AB）．

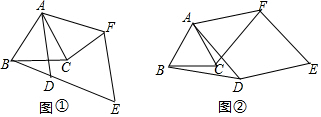
（1）如圖①，當AD與邊BC相交，點D與點F在直線AC的兩側時，BD與CF的數量關系為

．
（2）將圖①中的菱形ADEF繞點A旋轉α（0°＜α＜180°），如圖②．
Ⅰ．判斷（1）中的結論是否仍然成立，請利用圖②證明你的結論．
Ⅱ．若AC=4，AD=6，當△ACE為直角三角形時，直接寫出CE的長度．
組卷：365引用：4難度：0.1
解析
20．列方程解應用題：
小明和小剛約定周末到某體育公園打羽毛球．他們兩家到體育公園的距離分別是1200米，3000米，小剛騎自行車的速度是小明步行速度的3倍，若二人同時到達，則小明需提前4分鐘出發，求小明和小剛兩人的速度．
組卷：1131引用：16難度：0.8
解析
21．有甲、乙兩個不透明的布袋，甲袋中有兩個完全相同的小球，分別標有數字1和-2；乙袋中有三個完全相同的小球，分別標有數字-1、0和2．小麗先從甲袋中隨機取出一個小球，記錄下小球上的數字為x；再從乙袋中隨機取出一個小球，記錄下小球上的數字為y,設點P的坐標為（x,y）．
（1）請用表格或樹狀圖列出點P所有可能的坐標；
（2）求點P在一次函數y=x+1圖象上的概率．
組卷：1621引用：65難度：0.7
解析
22．已知菱形ABCD的邊長為1，∠ADC=60°，等邊△AEF兩邊分別交DC、CB于點E、F．
（1）特殊發現：如圖1，若點E、F分別是邊DC、CB的中點，求證：菱形ABCD對角線AC、BD的交點O即為等邊△AEF的外心；
（2）若點E、F始終分別在邊DC、CB上移動，記等邊△AEF的外心為P． ①猜想驗證：如圖2，猜想△AEF的外心P落在哪一直線上，并加以證明；②拓展運用：如圖3，當E、F分別是邊DC、CB的中點時，過點P任作一直線，分別交DA邊于點M，BC邊于點G，DC邊的延長線于點N，請你直接寫出
1
DM
+
1
DN
的值．
組卷：421引用：6難度：0.5
解析
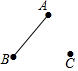23．如圖，C是線段AB外一點，按要求畫圖，
（1）畫射線CB；
（2）反向延長線段AB；
（3）連接AC，并延長AC至點D，使CD=AC．
組卷：82引用：2難度：0.5
解析

24．疫情期間，按照防疫要求，學生在進校時必須排隊接受體溫檢測．某校統計了學生早晨到校情況，發現學生到校的累計人數y（單位：人）可以看作時間x（單位：分鐘）的二次函數，其中0≤x≤30．統計數據如下表：

時間x（分鐘） 0 5 10 15 20 25 30

人數y（人） 0 275 500 675 800 875 900

（1）求出y與x之間的函數關系式．
（2）如果學生一進學校就開始測量體溫，測溫點有2個，每個測溫點每分鐘檢測20人，學生按要求排隊測溫．求第多少分鐘時排隊等待檢測體溫的人數最多？
（3）檢測體溫到第4分鐘后，為減少排隊等候時間，在校門口臨時增設1個人工體溫檢測點，已知人工每分鐘可檢測12人，人工檢測多長時間后，校門口不再出現排隊等待的情況（直接寫出結果）．

組卷：190引用：2難度：0.5

解析

25．計算：
（1）
3
-
27
+|
5
-4|+
5
-
（
-
6
）
2
；
（2）
x
2
-
1
x
+
3
÷（
10
-
2
x
x
+
3
+x-3）；
（3）
75
÷
3
+2
4
5
×
30
-（
2
-2
3
）²．
組卷：45引用：1難度：0.5
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

區縣	贛榆	東海	灌云	灌南	新浦	海州	連云港	開發區
成交量（套）	105	101	53	72	110	50	56	88

	得分
A	50＜n≤60
B	60＜n≤70
C	70＜n≤80
D	80＜n≤90
E	90＜n≤100

時間x（分鐘）	0	5	10	15	20	25	30
人數y（人）	0	275	500	675	800	875	900

2025年山東省青島市中考數學模擬試卷（七）

一、選擇題（本大題共9小題，每小題3分，共27分）

1．如圖，AB切圓O1于B點，AC切圓O2于C點，BC分別交圓O1、圓O2于D、E兩點．若∠BO1D=40°，∠CO2E=60°，則∠A的度數為何？（ ）

2．用科學記數法表示0.0000907，得（ ）

3．若實數x、y、z滿足（x-z）2-4（x-y）（y-z）=0，則下列式子一定成立的是（ ）

4．如圖，正五邊形ABCDE內接于圓O，點F是?EC上一點，則∠EFC的大小為（ ）

5．下列圖形中，既是軸對稱圖形又是中心對稱圖形的是（ ）

6．當a＜0時，2，2+a,2-a,a中最大的是（ ）

7．如圖，在平面直角坐標系中，△AOB為等腰直角三角形∠OAB=90°，邊OA在x軸正半軸上OA=2，點B在第一象限內，將△AOB繞點O順時針旋轉，每次旋轉45°則第2023次旋轉后，點B的坐標為（ ）

8．二次函數y=（x-1）2-2，若y隨x的增大而增大，則x的取值范圍是（ ）

9．如圖是三個大小不等的正方體拼成的幾何體，其中兩個較小正方體的棱長之和等于大正方體的棱長．該幾何體的主視圖、俯視圖和左視圖的面積分別是S1，S2，S3，則S1，S2，S3的大小關系是（ ）

二、填空題（本大題共6小題，每小題3分，共18分）

10．計算：cos245°+cos30°2sin60°+1-3?tan30°= ．

11．據市房管局統計，今年某周我市8個縣區的普通住宅成交量如下表：區縣贛榆東海灌云灌南新浦海州連云港開發區成交量（套）1051015372110505688則該周普通住宅成交量的中位數為 套．

12．爸爸，媽媽，小慧、小弟，這四人今年的年齡之和是99歲，爸爸比媽媽大4歲，小慧比小弟大3歲，9年前，他們的年齡之和為65歲，由以上條件可知今年爸爸歲．

13．如圖，六邊形ABCDEF為⊙O的內接正六邊形，若⊙O的半徑為23，則陰影部分的面積為 ．

14．如圖，在矩形ABCD中，AB=6cm,BC=8cm,若將矩形折疊，使點B與點D重合，則折痕EF的長為cm.

15．如圖，△ABC中，∠BAC=90°，AD⊥BC于D，若AB=4，BD=2，則BC=．

三、作圖題（本大題滿分4分）

四、解答題（本大題共9小題，共71分）

23．如圖，C是線段AB外一點，按要求畫圖，（1）畫射線CB；（2）反向延長線段AB；（3）連接AC，并延長AC至點D，使CD=AC．

25．計算：（1）3-27+|5-4|+5-（-6）2；（2）x2-1x+3÷（10-2xx+3+x-3）；（3）75÷3+245×30-（2-23）2．

1．如圖，AB切圓O₁于B點，AC切圓O₂于C點，BC分別交圓O₁、圓O₂于D、E兩點．若∠BO₁D=40°，∠CO₂E=60°，則∠A的度數為何？（　　）

2．用科學記數法表示0.0000907，得（　　）

3．若實數x、y、z滿足（x-z）²-4（x-y）（y-z）=0，則下列式子一定成立的是（　　）

4．如圖，正五邊形ABCDE內接于圓O，點F是
?
EC
上一點，則∠EFC的大小為（　　）

5．下列圖形中，既是軸對稱圖形又是中心對稱圖形的是（　　）

6．當a＜0時，2，2+a,2-a,a中最大的是（　　）

7．如圖，在平面直角坐標系中，△AOB為等腰直角三角形∠OAB=90°，邊OA在x軸正半軸上OA=2，點B在第一象限內，將△AOB繞點O順時針旋轉，每次旋轉45°則第2023次旋轉后，點B的坐標為（　　）

8．二次函數y=（x-1）²-2，若y隨x的增大而增大，則x的取值范圍是（　　）

9．如圖是三個大小不等的正方體拼成的幾何體，其中兩個較小正方體的棱長之和等于大正方體的棱長．該幾何體的主視圖、俯視圖和左視圖的面積分別是S₁，S₂，S₃，則S₁，S₂，S₃的大小關系是（　　）

10．計算：cos²45°+
cos
30
°
2
sin
60
°
+
1
-
3
?tan30°=

．

11．據市房管局統計，今年某周我市8個縣區的普通住宅成交量如下表：
區縣贛榆東海灌云灌南新浦海州連云港開發區
成交量（套） 105 101 53 72 110 50 56 88
則該周普通住宅成交量的中位數為

套．

12．爸爸，媽媽，小慧、小弟，這四人今年的年齡之和是99歲，爸爸比媽媽大4歲，小慧比小弟大3歲，9年前，他們的年齡之和為65歲，由以上條件可知今年爸爸
歲．

13．如圖，六邊形ABCDEF為⊙O的內接正六邊形，若⊙O的半徑為2
3
，則陰影部分的面積為

．

14．如圖，在矩形ABCD中，AB=6cm,BC=8cm,若將矩形折疊，使點B與點D重合，則折痕EF的長為
cm.

15．如圖，△ABC中，∠BAC=90°，AD⊥BC于D，若AB=4，BD=2，則BC=
．

23．如圖，C是線段AB外一點，按要求畫圖，
（1）畫射線CB；
（2）反向延長線段AB；
（3）連接AC，并延長AC至點D，使CD=AC．

25．計算：
（1）
3
-
27
+|
5
-4|+
5
-
（
-
6
）
2
；
（2）
x
2
-
1
x
+
3
÷（
10
-
2
x
x
+
3
+x-3）；
（3）
75
÷
3
+2
4
5
×
30
-（
2
-2
3
）²．