當前位置：試卷中心 > 試卷詳情

2024-2025學年上海市浦東新區三林中學北校八年級（下）月考數學試卷（5月份）

發布：2025/6/27 15:0:7

一、單項選擇題：（本大題共6題，每題2分，滿分12分）

1．已知正比例函數y=（k-3）x,若y隨x的增大而減小，則k的取值范圍是（　　）
A．k＞3 B．k＜3 C．k＞-3 D．k＜-3
組卷：10引用：3難度：0.5
解析
2．下列說法中，正確的是（　　）
A．菱形的對角線相等
B．兩組鄰邊分別相等的四邊形是菱形
C．對角線互相垂直的四邊形是菱形
D．菱形的對角線互相垂直平分
組卷：99引用：2難度：0.9
解析
3．若順次連接某四邊形四邊中點所得的四邊形是矩形，則原四邊形一定是（　　）
A．菱形 B．矩形
C．對角線互相垂直 D．對角線相等
組卷：348引用：6難度：0.7
解析
4．下列各式錯誤的是（　　）
A．|
0
|=0 B．
m
+（-
m
）=0 C．
m
+
n
=
n
+
m
D．
m
-
n
=
m
+（-
n
）
組卷：79引用：1難度：0.8
解析
5．下列方程中，有實數解的是（　　）
A．
x
x
-
1
=
1
x
-
1
B．
x
-
1
+2=0 C．
x
-
3
=1 D．
x
-
1
+
1
-
x
=1
組卷：34引用：2難度：0.5
解析
6．下列命題中，正確的是（　　）
A．有理數和數軸上的點一一對應
B．等腰三角形的對稱軸是它的頂角平分線
C．全等的兩個圖形一定成軸對稱
D．有理數和無理數統稱為實數
組卷：39引用：5難度：0.9
解析

二、填空題：（本大題共12題，每題3分，滿分36分）

7．如果直線y=2x+4與直線y=3x-b的交點在x軸上，那么b的值為
．
組卷：53引用：1難度：0.7
解析
8．如圖，已知矩形ABCD的邊AB=3，BC=9，將其折疊，使得點D與點B重合，折疊后折痕EF的長是

．
組卷：201引用：2難度：0.5
解析
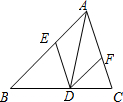9．如圖，在△ABC中，點D、E、F分別在BC、AB、AC上，且DE∥AC，DF∥AB．
（1）如果∠BAC=90°，那么四邊形AEDF是

形；
（2）如果AD是△ABC的角平分線，那么四邊形AEDF是

形．
組卷：428引用：6難度：0.7
解析
10．在△ABC中，∠C=90°，∠B=2∠A，則cosA=

．
組卷：40引用：2難度：0.7
解析
11．用換元法解方程
3
x
x
2
-
1
-
x
2
-
1
x
=
2
，如果設
y
=
x
x
2
-
1
，那么原方程可以化為關于y的整式方程為
．
組卷：121引用：3難度：0.8
解析
12．在平行四邊形ABCD中，
AD
=
a
，
AC
=
b
，則
AB
=
．
組卷：75引用：1難度：0.5
解析
13．立方根等于本身的實數是

．
組卷：185引用：4難度：0.9
解析
14．如圖，在△ABC中，點D、E、F分別是邊BC、AB、CA上的中點，且BC=6cm,AC=8cm,則四邊形CDEF的周長等于
cm.
組卷：7引用：1難度：0.7
解析
15．小明在計算多邊形內角和時，不小心漏掉了一個內角，其和為1160°，則漏掉的那個內角的度數是
．
組卷：15引用：1難度：0.6
解析
16．如果
2
3
9
x
+6
x
4
=20，那么x=
．
組卷：41引用：3難度：0.8
解析
17．如圖，是一個圓形花壇，中間的鮮花構成一個菱形圖案（單位：米），若每平方米種植鮮花20株，那么這個菱形圖案中共有鮮花
株．
組卷：56引用：2難度：0.7
解析
18．如圖，梯形ABCD的中位線EF的長為a,高為h,則圖中陰影部分的面積為

組卷：84引用：2難度：0.7
解析

三、解答題：（本大題共6題，滿分42分）

19．（1）如圖①，四邊形ABCD是中心對稱圖形，直線EF經過對稱中心O，則S_{四邊形AEFB}
S_{四邊形DEFC}（填“＞”“＜”“=”）；
（2）如圖②，正方形是中心對稱圖形，兩個正方形如圖所示擺放，O為小正方形對角線的交點，求作過點O的直線將整個圖形分成面積相等的兩部分．
組卷：128引用：4難度：0.5
解析
20．閱讀下面的材料，回答問題：
解方程x⁴-5x²+4=0，這是一個一元四次方程，根據該方程的特點，它的解法通常是：設x²=y,那么x⁴=y²，于是原方程可變為y²-5y+4=0①，解得y₁=1，y₂=4．
當y=1時，x²=1，∴x=±1；
當y=4時，x²=4，∴x=±2；
原方程有四個根：x₁=1，x₂=-1，x₃=2，x₄=-2．
（1）在由原方程得到方程①的過程中，利用
法達到
的目的，體現了數學的轉化思想．
（2）解方程：（x²+x）²-4（x²+x）-12=0
（3）已知非零實數a,b滿足a²-ab-12b²=0，求
a
b
的值．
組卷：317引用：2難度：0.7
解析
21．如圖，在直角梯形ABCD中，AD∥BC，∠B=90°，AD=24cm,BC=26cm,動點P從A點開始沿AD邊向D以3cm/s的速度運動，動點Q從點C開始沿CB邊向點以1cm/s的速度運動，點P、Q分別從A、C同時出發，設運動時間為t （s）．當其中一點到達端點時，另一點也隨之停止運動．
①當t為何值時，以CD、PQ為兩邊，以梯形的底（AD或BC）的一部分（或全部）為第三邊能構成一個三角形；
②求出當t為何值時，四邊形PQCD為等腰梯形．
組卷：182引用：2難度：0.1
解析
22．如圖，在正方形ABCD中，點F為對角線AC上一點，連接BF，DF．你能找出圖中的全等三角形嗎？選擇其中一對進行證明．
組卷：100引用：2難度：0.7
解析
23．用換元法解方程：x²-x-
12
x
2
-
x
=4．
組卷：715引用：2難度：0.6
解析
24．如圖1，直線l：
y
=
-
1
2
x
+
3
2
交x軸于點A，交y軸于點B，交直線m：y=x+3于點C，直線m交x軸于點D．
（1）求點A、點C的坐標；
（2）如圖1，點E為第一象限內直線l上一點，滿足△ACE的面積為6．
①求點E的坐標；
②線段PQ=1（點P在點Q的上方）為直線x=-1上的一條動線段，當EP+PQ+AQ的值最小時，求這個最小值及此時點P的坐標．
（3）如圖2，將直線l繞點C旋轉，在旋轉過程中，直線l交x軸于點M，是否存在某個時刻，使得△CDM為等腰三角形？若存在，求出線段OM的長度；若不存在，請說明理由．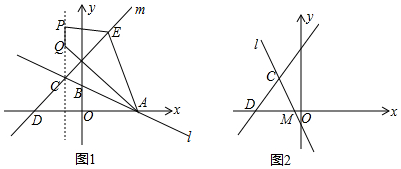
組卷：179引用：2難度：0.1
解析
25．我們知道，各類方程的解法雖然不盡相同，但是它們的基本思想都是“轉化”，即把未知轉化為已知．用“轉化”的數學思想，我們還可以解一些新方程．
認識新方程：
像
2
x
+
3
=x這樣，根號下含有未知數的方程叫做無理方程，可以通過方程兩邊平方把它轉化為2x+3=x²，解得x₁=3，x₂=-1．但由于兩邊平方，可能產生增根，所以需要檢驗，經檢驗，x₂=-1是原方程的增根，舍去，所以原方程的解是x=3．
運用以上經驗，解下列方程：
（1）
16
-
6
x
=x；
（2）x+2
x
-
3
=6．
組卷：965引用：6難度：0.1
解析