2020-2021學年江蘇省常州市高二（下）期中數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．角谷猜想，也叫3n+1猜想，是由日本數學家角谷靜夫發現的，是指對于每一個正整數，如果它是奇數，則對它乘3再加1；如果它是偶數，則對它除以2，如此循環最終都能夠得到1，如：取n=10，根據上述過程，得出10，5，16，8，4，2，1，共7個數．上述過程得到的7個整數中，隨機選取兩個不同的數，則兩個數都是奇數的概率為（　　）

  A． 1 15

  B． 2 15

  C． 1 21

  D． 2 21
  組卷：53引用：3難度：0.8

  解析

• 2．在二項式

  （

  x

  -

  y

  ）

  4

  的展開式中，有理項的項數為（　　）

  A．4

  B．3

  C．2

  D．1
  組卷：30引用：1難度：0.8

  解析

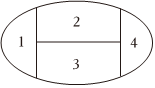• 3．用5種不同的顏色給圖中4個區域涂色，如果每個區域涂一種顏色，相鄰區域不能同色，那么涂色的方法有（　　）種

  A．120

  B．180

  C．240

  D．72
  組卷：48引用：1難度：0.7

  解析

• 4．已知函數f（x）=

  xlnx , x ＞ 0

  x e x ， x ≤ 0

  ，則函數y=f（x）的圖象大致是（　　）

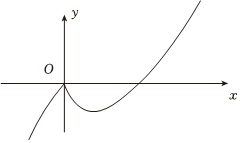
  A．	B．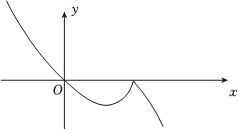
  C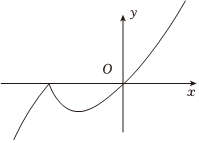．	D．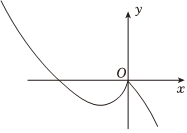
  組卷：179引用：2難度：0.8

  解析

• 5．已知隨機變量X～N（1，4），則P（1＜X＜5）=（　　）
  （參考數據P（μ-σ＜X≤μ+σ）=0.6826，P（μ-2σ＜X≤μ+2σ）=0.9544）

  A．0.6826

  B．0.3413

  C．0.9544

  D．0.4772
  組卷：8引用：2難度：0.8

  解析

• 6．2020年12月1日，某市開始實行生活垃圾分類管理，某單位有四個垃圾桶，分別是一個可回收物垃圾桶、一個有害垃圾桶、一個廚余垃圾桶、一個其它垃圾桶．因為場地限制，要將這四個垃圾桶擺放在三個固定角落，每個角落至少擺放一個，則不同的擺放方法共有（如果某兩個垃圾桶擺放在同一角落，它們的前后左右位置關系不作考慮）（　　）

  A．18種

  B．24種

  C．36種

  D．72種
  組卷：326引用：13難度：0.7

  解析

• 7．甲乙丙三名選手參加短跑、跳遠兩項比賽．每項比賽以后，隨機抽取一名選手進行興奮劑檢測．若每次檢測每位選手被抽到的概率相同，且每位選手最多被抽檢一次（第一次被抽檢的選手第二次免檢），則甲被抽檢的概率是（　　）

  A． 4 9

  B． 5 9

  C． 1 3

  D． 2 3
  組卷：17引用：2難度：0.6

  解析

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

• 21．某商場舉行有獎促銷活動，凡5月1日當天消費每超過400元（含400元），均可抽獎一次，抽獎箱里有6個形狀、大小、質地完全相同的小球（其中紅球有3個，白球有3個），抽獎方案設置兩種，顧客自行選擇其中的一種方案．
  方案一：從抽獎箱中，一次性摸出2個球，若摸出2個紅球，則打6折；若摸出1個紅球，則打8折；若沒摸出紅球，則不打折．
  方案二：從抽獎箱中，有放回地每次摸取1個球，連摸2次，每摸到1次紅球，立減100元．
  （1）若甲、乙消費均達到了400元，且均選擇抽獎方案一，試求他們其中有一人享受6折優惠的概率；
  （2）若丙消費恰好滿400元，試比較說明丙選擇哪種方案更劃算．
  組卷：23引用：1難度：0.6

  解析

• 22．已知e是自然對數的底數，函數f（x）=e^x+sinx-2x的導函數記為g（x），曲線y=f（x）在點A（a,f（a））處的切線l與y軸交于點（0，b）．
  （1）當a∈[-

  π

  2

  ，+∞）時，求實數b的取值范圍；
  （2）若對任意的x∈（0，+∞），都有g（x）＞x+m-3成立，求實數m的最大值．
  組卷：9引用：1難度：0.5

  解析