當前位置：試卷中心 > 試卷詳情

2021-2022學年山東省濟寧二中高二（上）期中數學試卷

發布：2024/4/20 14:35:0

一、單項選擇題：本大題共8小題，每小題5分，共40分．在每小題只有一項是符合題目要求的．

1．直線
3
x
+
3
y
+
1
=
0
的傾斜角α=（　　）
A．30° B．60° C．120° D．150°
組卷：313引用：15難度：0.9
解析
2．如圖，在空間四邊形ABCD中，設E，F分別是BC，CD的中點，則
AD
+
1
2
（
DB
+
DC
）
=（　　）
A．
AD
B．
FA
C．
AE
D．
EF
組卷：100引用：4難度：0.8
解析
3．已知橢圓
x
2
25
+
y
2
9
=
1
上的一點P到橢圓一個焦點的距離為4，則P到另一焦點距離為（　　）
A．5 B．4 C．6 D．7
組卷：23引用：3難度：0.9
解析
4．已知圓的一條直徑的兩個端點分別在x軸和y軸上，圓心坐標為（-3，-2），則此圓的方程是（　　）
A．（x-3）²+（y-2）²=13 B．（x+3）²+（y+2）²=13
C．（x-3）²+（y-2）²=52 D．（x+3）²+（y+2）²=52
組卷：56引用：4難度：0.7
解析
5．設a∈R，則“a=1”是“直線l₁：ax+2y-1=0與直線l₂：x+（a+1）y+4=0平行”的（　　）
A．必要不充分條件 B．充分不必要條件
C．充分必要條件 D．既不充分也不必要條件
組卷：722引用：108難度：0.9
解析
6．已知點A（-2，3）在拋物線C：y²=2px的準線上，記C的焦點為F，則直線AF的斜率為（　　）
A．-
4
3
B．-1 C．-
3
4
D．-
1
2
組卷：2139引用：23難度：0.9
解析
7．在下列命題中：
①若向量
a
，
b
共線，則向量
a
，
b
所在的直線平行；
②若向量
a
，
b
所在的直線為異面直線，則向量
a
，
b
一定不共面；
③若三個向量
a
，
b
，
c
兩兩共面，則向量
a
，
b
，
c
共面；
④已知是空間的三個向量
a
，
b
，
c
，則對于空間的任意一個向量
p
總存在實數x,y,z使得
p
=
x
a
+
y
b
+
z
c
；
其中正確的命題的個數是（　　）
A．0 B．1 C．2 D．3
組卷：331引用：25難度：0.9
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本大題共6小題，共70分.解答應寫出必要的文字說明、證明過程或演算步驟.

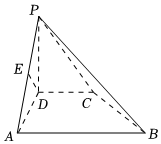21．在四棱錐P-ABCD中，PD⊥平面ABCD，AB∥DC，AB⊥AD，
CD
=
AD
=
1
2
AB
，∠PAD=45°，E是PA的中點，G在線段AB上，且滿足CG⊥BD．
（1）求證：DE∥平面PBC；
（2）求平面PGC與平面BPC夾角的余弦值；
（3）在線段PA上是否存在點H，使得GH與平面PGC所成角的正弦值是
3
3
，若存在，求出AH的長；若不存在，請說明理由．
組卷：333引用：10難度：0.5
解析
22．已知拋物線C的標準方程為y²=2px（p＞0），M為拋物線C上一動點，A（a,0）（a≠0）為其對稱軸上一點，直線MA與拋物線C的另一個交點為N．當A為拋物線C的焦點且直線MA與其對稱軸垂直時，△MON的面積為
9
2
．
（Ⅰ）求拋物線C的標準方程；
（Ⅱ）記t=
1
|
AM
|
+
1
|
AN
|
，若t值與M點位置無關，則稱此時的點A為“穩定點”，試求出所有“穩定點”，若沒有，請說明理由．
組卷：336引用：9難度：0.1
解析