當前位置：試卷中心 > 試卷詳情

2022-2023學年寧夏銀川二中高一（上）期末數學試卷

發布：2024/4/20 14:35:0

1．已知全集U={1，2，3，4，5，6}，A={2，4，6}，則?_UA=（　　）
A．{2，4，6} B．{1，3，5} C．{2，4，5} D．{2，5}
組卷：47引用：2難度：0.8
解析

2．下列說法中正確的是（　　）

A．命題“?x₀∈R，

＞

”的否定是“?x∈R，x²-x≤0”

B．若a＞b＞0，且c＞0，則

＞

C．“ac²＞bc²”的充要條件是“a＞b”

D．函數

sinx

（

∈

（

，

]

）

的最小值為4

組卷：24引用：1難度：0.6

3．設a=2^0.3，b=0.3²，c=log₂0.3，則a,b,c的大小關系是（　　）
A．a＜b＜c B．b＜c＜a C．c＜a＜b D．c＜b＜a
組卷：1347引用：82難度：0.9
解析
4．下列四個函數中，以π為最小正周期，且在區間
（
π
2
，
π
）
上單調遞減的是（　　）
A．y=sin|x| B．y=cosx C．y=-tanx D．
y
=
sin
x
2
組卷：127引用：1難度：0.8
解析
5．國家速滑館又稱“冰絲帶”，是北京2022年冬奧會的標志性場館，擁有亞洲最大的全冰面設計，但整個系統的碳排放接近于零，做到了真正的智慧場館、綠色場館，并且為了倡導綠色可循環的理念，場館還配備了先進的污水、雨水過濾系統，已知過濾過程中廢水的污染物數量N（mg/L）與時間t的關系為
N
=
N
0
e
-
kt
（N₀為最初污染物數量）．如果前2個小時消除了20%的污染物，那么前6個小時消除了污染物的（　　）
A．51.2% B．48.8% C．52% D．48%
組卷：63引用：3難度：0.6
解析
6．已知
sin
（
α
-
π
4
）
=
1
3
，則
cos
（
5
π
4
+
α
）
等于（　　）
A．
-
1
3
B．
1
3
C．
2
2
3
D．
-
2
2
3
組卷：389引用：1難度：0.8
解析
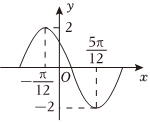7．函數y=Asin（ωx+φ）在一個周期內的圖像如圖，則此函數的解析式為（　　）
A．
y
=
2
sin
（
2
x
+
2
π
3
）
B．
y
=
2
sin
（
2
x
+
π
3
）
C．
y
=
2
sin
（
1
2
x
-
π
3
）
D．
y
=
2
sin
（
2
x
-
π
3
）
組卷：889引用：5難度：0.8
解析

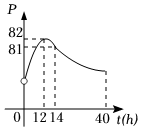21．某專家研究高一學生上課注意力集中的情況，發現其注意力指數p與聽課時間t（h）之間的關系滿足如圖所示的曲線．當t∈（0，14]時，曲線是二次函數圖象的一部分，當t∈（14，40]時，曲線是函數y=log_a（t-5）+83（0＜a＜1）圖象的一部分．專家認為，當注意力指數p大于或等于80時定義為聽課效果最佳．
（1）試求p=f（t）的函數關系式．
（2）若不是聽課效果最佳，建議老師多提問，增加學生活動環節，問在哪一個時間段建議老師多提問，增加學生活動環節？請說明理由．
組卷：69引用：8難度：0.6
解析
22．已知函數f（x）=sin（ωx+φ）-1（ω＞0，0＜φ＜π）的圖象兩鄰對稱軸之間的距離是
π
2
，若將f（x）的圖象先向右平移
π
6
單位，再向上平移1個單位，所得函數g（x）為奇函數．
（1）求函數f（x）的解析式；
（2）若對任意
x
∈
[
0
，
π
3
]
，f²（x）-（2+m）f（x）+2+m≤0恒成立，求實數m的取值范圍；
（3）若函數h（x）=2f（x）+3的圖象在區間[a,b]（a,b∈R且a＜b）上至少含有30個零點，在所有滿足條件的區間[a,b]上，求b-a的最小值．
組卷：608引用：7難度：0.3
解析