2023-2024學年北京市朝陽區陳經綸中學高二(上)開學數學試卷
發布:2024/8/21 4:0:1
一.選擇題(共10小題,每小題4分,共40分,在每小題列出的四個選項中,選出符合題目要求的一項)
-
1.設集合A={z|z 為虛數},B={z|z為純虛數},C={z|z為復數},則A,B,C間的關系為( )
A.A?B?C B.B?A?C C.B∈C?A D.A∈C?B 組卷:66引用:1難度:0.9 -
2.已知A(0,1),B(3,-2),且
,則AC=2CB的坐標為( )ACA.(2,-1) B.(6,-5) C.(6,-6) D.(2,-2) 組卷:222引用:2難度:0.8 -
3.某市6月前10天的空氣質量指數為35,54,80,86,72,85,58,125,111,53,則這組數據的第70百分位數是( )
A.86 B.85.5 C.85 D.84.5 組卷:387引用:3難度:0.8 -
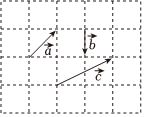 4.向量,a,b在正方形網格中的位置如圖所示,若向量c,則λ+μ的值等于( )c=λa+μb
4.向量,a,b在正方形網格中的位置如圖所示,若向量c,則λ+μ的值等于( )c=λa+μbA.1 B.-1 C.3 D.-3 組卷:102引用:2難度:0.8 -
5.將函數y=sinx+cosx的圖象向右平移
個單位,所得圖象的函數解析式為y=( )π2A.-sinx+cosx B.-cosx+sinx C.-sinx-cosx D.sinx+cosx 組卷:83引用:2難度:0.7 -
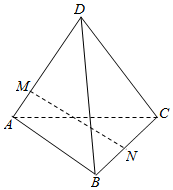 6.已知四面體ABCD,=DA,a=DB,b=DC,點M在棱DA上,c=3DM,N為BC中點,則MA=( )MN
6.已知四面體ABCD,=DA,a=DB,b=DC,點M在棱DA上,c=3DM,N為BC中點,則MA=( )MNA.- 34-a12-b12cB. 34+a12+b12cC.- 34+a12+b12cD. 34-a12-b12c組卷:683引用:9難度:0.7 -
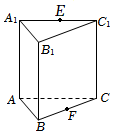 7.如圖,在直三棱柱ABC-A1B1C1中,點E,F分別是棱A1C1,BC的中點,則下列結論中不正確的是( )
7.如圖,在直三棱柱ABC-A1B1C1中,點E,F分別是棱A1C1,BC的中點,則下列結論中不正確的是( )A.CC1∥平面A1ABB1 B.AF∥平面A1B1C1 C.EF∥平面A1ABB1 D.AE∥平面B1BCC1 組卷:1140引用:7難度:0.7
三.解答題(共6小題,共85分)
-
20.在△ABC中,
.2cos2B2-2sinB2cosB2=1
(Ⅰ)求∠B;
(Ⅱ)再從下列三個條件中,選擇兩個作為已知,使得△ABC存在且唯一,求△ABC的面積.
條件①:;cosA=-12
條件②:;b=2
條件③:AB邊上的高為.62組卷:252引用:5難度:0.6 -
21.設m,n∈N*,已知由自然數組成的集合S={a1,a2,…,an}(a1<a2<?<an),集合S1,S2,…,Sm是S的互不相同的非空子集,定義n×m數表:
X=,其中xij=x11x12…x1mx21x22…x2m????xn1xn2…xnm,1,ai∈Sj0,ai?Sj
設 d(ai)=xi1+xi2+?+xim(i=1,2,?,n),令d(S)是 d(a1),d(a2),…d(an) 中的最大值.
(Ⅰ)若m=3,S={1,2,3},且X=,求S1,S2,S3及d(S);101011100
(Ⅱ)若S={1,2,…,n},集合S1,S2,…,Sn中的元素個數均相同,若d(S)=3,求n的最小值;
(Ⅲ)若 m=7,S={1,2,…,7},集合 S1,S2,…,S7 中的元素個數均為3,且Si∩Sj≠?(1≤i<j≤7),求證:d(S)的最小值為3.組卷:108引用:2難度:0.2


