2023-2024學(xué)年上海市楊浦區(qū)復(fù)旦大學(xué)附中高二（上）期中數(shù)學(xué)試卷（A卷）

一、填空題（本大題共有12小題，第1-6題每題4分，第7-12題每題5分，滿分54分）考生應(yīng)在答題紙的相應(yīng)位置直接填寫結(jié)果.

• 1．直線2x-y-1=0的傾斜角的大小為

  ．
  組卷：37引用：4難度：0.8

  解析

• 2．拋物線y²=-24x的準(zhǔn)線方程是

  ．
  組卷：91引用：3難度：0.9

  解析

• 3．直線l經(jīng)過點P（-1，2），且與直線2x-3y+4=0平行，則直線l的方程為

  ．
  組卷：41引用：3難度：0.9

  解析

• 4．橢圓

  x

  2

  4

  +

  y

  2

  5

  =

  1

  的離心率是

  ．
  組卷：64引用：3難度：0.7

  解析

• 5．過點（5，3）作圓（x-3）²+y²=4的切線，則切線的方程為

  ．
  組卷：131引用：4難度：0.5

  解析

• 6．在△ABC中，A（-3，0），B（3，0），3sinB-3sinA=sinC，則頂點C的軌跡方程是

  ．
  組卷：2引用：6難度：0.7

  解析

• 7．直線

  x = - t

  y = 1 + 2 t

  （t為參數(shù)，t∈R）和曲線

  C

  ：

  x = 2 cosθ

  y = 2 sinθ

  ，（θ為參數(shù)，θ∈R）交于P、Q兩點，則|PQ|=

  ．
  組卷：19引用：2難度：0.7

  解析

三、解答題（本大題共5題，滿分78分）解答下列各題須在答題紙的相應(yīng)位置寫出必要的步驟.

• 20．已知直線x+y+

  3

  =0與橢圓E：

  x

  2

  a

  2

  +

  y

  2

  =1有且只有一個公共點．
  （1）求橢圓E的方程；
  （2）是否存在實數(shù)λ，使橢圓E上存在不同兩點P、Q關(guān)于直線2x-y-λ=0對稱？若存在，求λ的取值范圍；若不存在，請說明理由；
  （3）橢圓E的內(nèi)接四邊形ABCD的對角線AC與BD垂直相交于橢圓的左焦點，S是四邊形ABCD的面積，求S的最小值．
  組卷：106引用：3難度：0.4

  解析

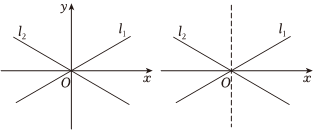• 21．平面上，直線l₁和l₂相交于點O，它們的夾角為2θ．已知動點P到直線l₁與l₂的距離之積為定值m²（m＞0），動點P的軌跡記為曲線E．我們以O(shè)為坐標(biāo)原點，以直線l₁與l₂夾角的平分線為x軸，建立直角坐標(biāo)系，如圖．
  （1）求曲線E的方程；
  （2）當(dāng)m=1，

  θ

  =

  π

  4

  時，直線l與曲線E順次交于A、B、C、D四點，求證：

  AB

  =

  CD

  ；
  （3）當(dāng)

  m

  =

  12

  5

  ，

  θ

  =

  arctan

  3

  4

  時，是否存在直線l與曲線E只有A、B、C三個不同公共點（點B在線段AC上），使得

  OA

  ⊥

  OC

  ？若存在，求出直線l的方程；若不存在，請說明理由．
  組卷：37引用：3難度：0.3

  解析