2022-2023學年福建省寧德市高二（上）期末數學試卷

一、單項選擇題（本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一個選項是符合題目要求的）

• 1．若直線l經過點

  A

  （

  -

  1

  ，

  3

  ）

  ，

  B

  （

  -

  2

  ，

  2

  3

  ）

  ，則直線l的傾斜角為（　　）

  A．30°

  B．60°

  C．120°

  D．150°
  組卷：162引用：3難度：0.8

  解析

• 2．雙曲線

  x

  2

  2

  -

  y

  2

  4

  =1的漸近線方程為（　　）

  A．y=±2x

  B．y=± 2 x

  C．y=± 1 2 x

  D．y=± 2 2 x
  組卷：85引用：10難度：0.9

  解析

• 3．圓

  O

  1

  ：

  （

  x

  +

  1

  ）

  2

  +

  y

  2

  =

  1

  與圓

  O

  2

  ：

  x

  2

  +

  y

  2

  -

  2

  3

  y

  -

  1

  =

  0

  的位置關系為（　　）

  A．內切

  B．相交

  C．外切

  D．外離
  組卷：133引用：2難度：0.8

  解析

• 4．數列{a_n}的前n項之和為S_n=n²+2n,那么a₆=（　　）

  A．11

  B．12

  C．13

  D．14
  組卷：74引用：4難度：0.7

  解析

• 5．已知動圓M經過點A（3，0），且與直線l：x=-3相切，則動圓圓心M的軌跡方程為（　　）

  A．y2=12x

  B．y2=-12x

  C．x2=12y

  D．x2=-12y
  組卷：80引用：1難度：0.8

  解析

• 6．將5名北京冬奧會志愿者分配到花樣滑冰、短道速滑、冰球和冰壺4個項目進行培訓，每名志愿者只分配到1個項目，每個項目至少分配1名志愿者，則不同的分配方案共有（　　）

  A．60種

  B．120種

  C．240種

  D．480種
  組卷：8106引用：51難度：0.8

  解析

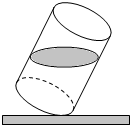• 7．如圖所示，一只裝有半杯水的圓柱形水杯，將其傾斜使杯底與水平桌面成30°，此時杯內水面成橢圓形，此橢圓的離心率為（　　）

  A． 3 2

  B． 3 4

  C． 1 2

  D． 1 4
  組卷：142引用：5難度：0.9

  解析

四、解答題：（本大題共6小題，共70分.解答應寫出文字說明，證明過程或演算步驟.）

• 21．已知數列{a_n}前n項和為S_n，a₂=2，S_n=a_n+1-1．
  （1）求數列{a_n}的通項公式；
  （2）若b_n=（2n-3）a_n，求數列{b_n}的前n項和T_n；
  （3）

  ?

  n

  ∈

  N

  *

  ，

  λ

  ＞

  T

  n

  -

  5

  4

  n

  恒成立，求實數λ的范圍．
  組卷：80引用：2難度：0.4

  解析

• 22．雙曲線

  E

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  ，恰好過

  P

  1

  （

  -

  2

  3

  ，

  2

  ）

  ，

  P

  2

  （

  3

  ，

  0

  ）

  ，

  P

  3

  （

  2

  3

  ，

  1

  ）

  ，

  P

  4

  （

  2

  3

  ，-

  1

  ）

  中的三點．
  （1）求雙曲線E的方程；
  （2）記雙曲線E上不同的三點A，B，C，其中A為雙曲線的右頂點，若直線AB，AC的斜率之積為1，證明：直線BC過定點．
  組卷：91引用：2難度：0.5

  解析