2023-2024學年浙江省杭州地區（含周邊）重點中學高二（上）期中數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．直線

  x

  -

  3

  y

  -

  1

  =

  0

  的傾斜角為（　　）

  A． π 6

  B． π 3

  C． 2 π 3

  D． 5 π 6
  組卷：109引用：20難度：0.7

  解析

• 2．某班共有45名學生，其中女生25名，為了解學生的身體狀況，現采用分層抽樣的方法進行調查，若樣本中有5名女生，則樣本中男生人數為（　　）

  A．4

  B．5

  C．6

  D．9
  組卷：140引用：2難度：0.9

  解析

• 3．在平行六面體ABCD-A₁B₁C₁D₁中，若

  DM

  =

  1

  3

  D

  D

  1

  ，則

  MB

  =（　　）

  A． 1 3 A A 1 + AD - AB	B． - 1 3 A A 1 - AD + AB
  C． - 2 3 A A 1 + AD - AB	D． 2 3 A A 1 - AD + AB
  組卷：101引用：2難度：0.8

  解析

• 4．已知向量

  a

  2

  =

  3

  ，

  b

  =（2，0），

  |

  a

  +

  b

  |

  =

  1

  ，則

  a

  與

  b

  的夾角等于（　　）

  A． π 6

  B． π 3

  C． 2 π 3

  D． 5 π 6
  組卷：94引用：3難度：0.7

  解析

• 5．甲、乙兩同學對同一組數據進行分析，甲同學得到的數據均值為

  x

  ，方差為s²，乙同學不小心丟掉了一個數據，得到的均值仍為

  x

  ，方差為2，則下列判斷正確的是（　　）

  A．s2=2

  B．s2＞2

  C．s2＜2

  D．s2與2的大小關系無法判斷
  組卷：243引用：4難度：0.5

  解析

• 6．已知圓C：（x-1）²+y²=4，直線l：x-my+2m=0與圓C相交于A、B兩點，若圓C上存在點P，使得△ABP為正三角形，則實數m的值為（　　）

  A． m = - 4 3

  B． m = 4 3

  C．m=- 4 3 或m=0

  D． m = 4 3 或m=0
  組卷：118引用：4難度：0.5

  解析

• 7．棱長為2的正方體ABCD-A₁B₁C₁D₁中，點N在以A為球心半徑為1的球面上，點M在平面ABCD內且C₁M與平面ABCD所成角為60°，則M，N兩點間的最近距離是（　　）

  A． 2 2 - 2 3 3

  B． 2 2 - 2 3 3 - 1

  C． 2 3 - 1

  D． 2 3 - 2 2
  組卷：59引用：1難度：0.5

  解析

四、解答題：本題包括6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

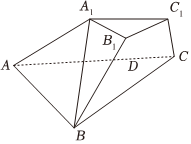• 21．如圖，三棱臺ABC-A₁B₁C₁中，A₁C₁=2，AC=3，D為線段AC上靠近C的三等分點．
  （1）在線段BC上求一點E，使A₁B∥平面C₁DE，并求

  BE

  BC

  的值；
  （2）若AA₁=AB=2，∠A₁AC=∠BAC=

  π

  3

  ，點A₁到平面ABC的距離為

  3

  2

  ，且點A₁在底面ABC的射影落在△ABC內部，求直線B₁D與平面ACC₁A₁所成角的正弦值．
  組卷：93引用：1難度：0.5

  解析

• 22．已知圓O：x²+y²=1和直線l：x+y-2=0，圓P以點（-1，-2）為圓心，且被直線l截得的弦長為

  14

  ．
  （1）求圓P的方程；
  （2）設M為圓P上任意一點，過點M向圓O引切線，切點為N，試探究：平面內是否存在一定點R，使得

  |

  MN

  |

  2

  |

  MR

  |

  2

  為定值？若存在，請求出定點R的坐標，并指出相應的定值：若不存在，請說明理由．
  組卷：99引用：2難度：0.5

  解析