當前位置：試卷中心 > 試卷詳情

2022-2023學年北京工業大學附中高二（上）月考數學試卷（10月份）

發布：2024/9/22 9:0:8

1．直線x+
3
y-2=0的傾斜角為（　　）
A．
π
6
B．
π
4
C．
π
3
D．
5
π
6
組卷：438引用：38難度：0.8
解析
2．若A（-1，-2），B（4，8），C（5，x），且A，B，C三點共線，則x=（　　）
A．-2 B．5 C．10 D．12
組卷：393引用：10難度：0.8
解析
3．某直線l過點B（-3，4），且在x軸上的截距是在y軸上截距的2倍，則該直線的斜率是（　　）
A．
-
4
3
B．
-
1
2
C．
4
3
或
-
1
2
D．
-
4
3
或
-
1
2
組卷：466引用：3難度：0.8
解析
4．已知直線l₁：x+y-1=0，l₂：x+m²y=0，則“m=1”是“l₁∥l₂”的（　　）
A．充分不必要條件 B．必要不充分條件
C．充分必要條件 D．既不充分也不必要條件
組卷：244引用：5難度：0.8
解析
5．已知點A（3，-1，0），若向量
AB
=
（
2
，
5
，-
3
）
，則點B的坐標是（　　）
A．（1，-6，3） B．（5，4，-3） C．（-1，6，-3） D．（2，5，-3）
組卷：1000引用：21難度：0.7
解析
6．若
a
=（2，3，m），
b
=（2n,6，8）且
a
，
b
為共線向量，則m+n的值為（　　）
A．7 B．
5
2
C．6 D．8
組卷：234引用：8難度：0.9
解析

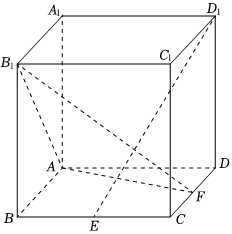18．如圖，在棱長為1的正方體ABCD-A₁B₁C₁D₁中，點E、F分別為棱BC、CD中點．
（1）求證：D₁E⊥平面AB₁F；
（2）求直線AB與平面AB₁F所成角的正弦值．
組卷：23引用：1難度：0.5
解析
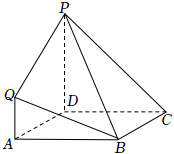19．在如圖所示的幾何體中，四邊形ABCD是正方形，四邊形ADPQ是梯形，PD∥QA，
∠
PDA
=
π
2
，平面ADPQ⊥平面ABCD，且AD=PD=2QA=2．
（1）求證：QB∥平面PDC；
（2）求平面CPB與平面PBQ所成角的大小；
（3）已知點H在棱PD上，且異面直線AH與PB所成角的余弦值為
7
3
15
，求點A到平面HBC的距離．
組卷：652引用：5難度：0.6
解析