2022年黑龍江省大慶中學(xué)高考數(shù)學(xué)二模試卷（理科）

一、選擇題（本大題共12小題，每小題5分，共60分．在每小題給出的四個(gè)選項(xiàng)中，只有一個(gè)選項(xiàng)是符合題目要求的）

• 1．已知集合A={x∈Z|-2≤x＜4}，B={x|log₂（x+1）＜2}，則A∩B的元素個(gè)數(shù)為（　　）

  A．3

  B．4

  C．5

  D．6
  組卷：80引用：1難度：0.8

  解析

• 2．已知復(fù)數(shù)z=

  1

  -

  i

  2021

  1

  +

  i

  ，則

  z

  的虛部是（　　）

  A．-1

  B．-i

  C．1

  D．i
  組卷：344引用：8難度：0.8

  解析

• 3．在空間中，已知命題p：△ABC的三個(gè)頂點(diǎn)到平面α的距離相等且不為零，命題q：平面α∥平面ABC，則p是q的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：326引用：6難度：0.6

  解析

• 4．已知數(shù)列{a_n}是首項(xiàng)為a₁，公差為d的等差數(shù)列，前n項(xiàng)和為S_n，滿足2a₄=a₃+5，則S₉=（　　）

  A．35

  B．40

  C．45

  D．50
  組卷：422引用：15難度：0.7

  解析

• 5．在流行病學(xué)中，基本傳染數(shù)是指每名感染者平均可傳染的人數(shù)．當(dāng)基本傳染數(shù)高于1時(shí)，每個(gè)感染者平均會(huì)感染1個(gè)以上的人，從而導(dǎo)致感染這種疾病的人數(shù)呈指數(shù)級(jí)增長(zhǎng)．當(dāng)基本傳染數(shù)持續(xù)低于1時(shí)，疫情才可能逐漸消散．接種新冠疫苗是預(yù)防新冠病毒感染、降低新冠肺炎發(fā)病率和重癥率的有效手段．已知新冠病毒的基本傳染數(shù)R₀=4，若1個(gè)感染者在每個(gè)傳染期會(huì)接觸到N個(gè)新人，這N人中有V個(gè)人接種過疫苗（

  V

  N

  稱為接種率），那么1個(gè)感染者新的傳染人數(shù)為

  R

  0

  N

  （N-V），為了有效控制新冠疫情（使1個(gè)感染者傳染人數(shù)不超過1），我國(guó)疫苗的接種率至少為（　　）

  A．75%

  B．80%

  C．85%

  D．90%
  組卷：140引用：4難度：0.9

  解析

• 6．已知平面向量

  a

  ，

  b

  滿足|

  a

  |=2，|

  b

  |=1，且

  a

  與

  b

  的夾角為

  2

  π

  3

  ，則|

  a

  +

  b

  |=（　　）

  A． 3

  B． 5

  C． 7

  D．3
  組卷：724引用：6難度：0.8

  解析

• 7．設(shè)m∈（0，1），若a=lgm,b=lgm²，c=（lgm）²，則（　　）

  A．a(chǎn)＞b＞c

  B．b＞c＞a

  C．c＞a＞b

  D．c＞b＞a
  組卷：940引用：15難度：0.7

  解析

三、解答題（本大題共7小題，共70分．解答應(yīng)寫出文字說明、證明過程或演算步驟）

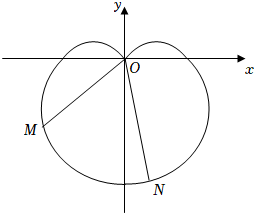• 22．如圖，在直角坐標(biāo)系中，以原點(diǎn)O為極點(diǎn)，x軸正半軸為極軸建立極坐標(biāo)系．圖中的心型曲線C₁的極坐標(biāo)方程為ρ=1-sinθ（0≤θ＜2π，ρ≥0），M為曲線C₁上一動(dòng)點(diǎn)，曲線C₂的參數(shù)方程為

  x = tcosα

  y = tsinα

  （t為參數(shù)，0≤α＜π）．
  （1）若C₁與C₂交于A、O、B三點(diǎn)，證明：|AB|為定值；
  （2）射線OM逆時(shí)針旋轉(zhuǎn)

  π

  3

  后與C₁交于點(diǎn)N，求|OM|+|ON|的最大值．
  組卷：135引用：3難度：0.6

  解析

• 23．已知函數(shù)f（x）=|x-a|+|x+3|．
  （1）當(dāng)a=1時(shí)，求不等式f（x）≥6的解集；
  （2）若f（x）＞-a,求a的取值范圍．
  組卷：1794引用：12難度：0.7

  解析