2008-2009學年浙江省臺州市高二（下）期末信息技術試卷（2）（選考）
發布：2024/4/20 14:35:0
一、選擇題：本大題13小題，每小題2分，共26分．每小題給出的四個選項中，只有一個符合題目要求，請將其代碼填寫在答題卡上相應的位置．錯選、多選或未選均不得分．
-
1．下列關于算法的說法中正確的是（ ）
①求解某一類問題的算法是唯一的；
②算法必須在有限步操作之后結束；
③算法的每一步操作必須是明確無歧義的；
④算法必須有輸入、輸出．組卷：11引用：3難度：0.9 -
2．下列Visual Basic程序段運行后，變量Max的值為（ ）
a=3：b=10：max=0
if a＞0then max=3
if b＞0then max=10．組卷：7引用：2難度：0.9 -
3．在Visual Basic中，每個控件都具有的屬性是（ ）
組卷：3引用：3難度：0.9 -
4．下列選項中可以用在Visual Basic中作累加器變量名的是（ ）
組卷：6引用：1難度：0.7 -
5．下列Visual Basic表達式正確的是（ ）
組卷：5引用：1難度：0.7 -
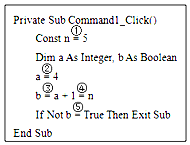6．“=”在Visual Basic程序中既可以表示賦值操作，也可以表示關系運算．如圖程序段中“=”作用和⑤相同的是（ ）組卷：5引用：1難度：0.7
二、綜合題：本大題5小題，其中第14題2分，第15題3分，第16題4分，第17題4分，第18題6分，共19分．
-
17．用計算機解決“兔子繁殖問題”．
題目描述：一對兔子飼養到第二個月進入成年，從第三個月開始每個月生一對小兔子，所生小兔子也是出生后第二個月成年，從第三個月開始每月生一對小兔子．假設兔子不會死亡，問這樣下去一年后有多少對兔子？
題目分析：設第n個月兔子的數量用Sn表示．第一、二個月兔子沒有繁殖能力，所以還是一對，即S1=1，S2=1；第三個月，生下一對小兔子，兔子數量達到2對，即S3=2；第四個月大兔子繼續生下一對小兔子，第三個月出生的小兔子進入成年期但還沒生育，兔子數量再加1對，即S4=3；第五個月老兔子繼續生育，前個月（第三月）出生的小兔子也開始生育，上個月（第四月）出生的小兔子成年，兔子數量加2對，即S5=5；…依此類推可以列出表：
可以發現如下規律：除第1、2個月兔子數量為1對外，第n個月的兔子數量等于前兩個月的兔子數量之和，即Sn=Sn-2+Sn-1．如果將每月兔子數量看作數列的各項，就構成了數學史上一個有名的數列，即“斐波拉契數列”：1、1、2、3、5、8、13、21、34、55…這個數列有許多奇特的性質，例如，從第3個數起，每個數與它后面那個 數的比值，都很接近于0.618，正好與大名鼎鼎的“黃金分割”相吻合．經過月數 1 2 3 4 5 6 7 8 9 … 兔子對數 1 1 2 3 5 8 13 21 34 …
（1）為解決此題，我們采用了算法．（填：枚舉、解析、排序、查找）
（2）Visual Basic程序界面設計如圖所示（圖一為對象初始屬性，圖二為修改對象屬性后界面）．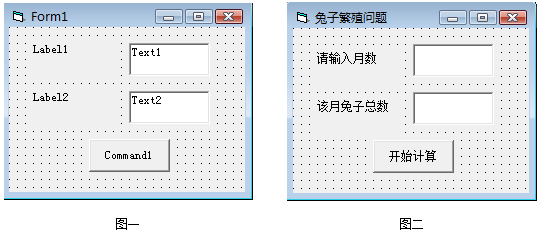
根據圖，如表A、B分別代表的屬性名分別是、．
（3）假設程序編寫已經正確完成，運行后出現如圖二窗口．當在上邊文本框輸入12，則點擊“開始計算”按鈕后，下邊文本框中顯示的內容是：對象名稱 對象屬性 屬性值 Form1 A 兔子繁殖問題 Text1 B （空白） ．組卷：2引用：1難度：0.3 -
18．利用輾轉相除法求最大公約數．
輾轉相除法，又名歐幾里德算法，是求兩個正整數最大公約數的算法，它的出現可追溯至3000年前．輾轉相除法并不需要把數作質因子分解．用輾轉相除法求正整數a、b的最大公約數運算過程為：
第一步：用被除數a除以除數b,得到余數c；
第二步：如果余數c不為0，則用上一步的除數b替換被除數a,用上一步的余數c替換除數b,再次執行第一步；如果余數為0則執行下一步；
第三步：則此時的除數即是a、b最大公約數．
例如a=60，b=25，運算過程為：
①60÷25=2…10；②25÷10=2…5；③10÷5=2…0．第③步時，余數為0，運算結束，則此步的除數5即是60和25的最大公約數．
（1）根據以上分析，畫出“輾轉相除法求最大公約數”算法流程圖如圖．其中編號①處應畫內容為，編號②處應畫內容為．
（2）Visual Basic代碼實現：
Private Sub Command1_Click（ ）
Dim a As Integer,b As Integer
Dim③
a=Val（Text1．Text）
b=Val（Text2．Text）
c=a Mod b
Do While④
a=b
b=c
c=a Mod b
Loop
Text3．Text=Str（b）
End Sub
其中③、④空白處應填的代碼分別是：
③；④．組卷：2引用：1難度：0.3