2022-2023學(xué)年遼寧省沈陽120中高二（上）第三次月考數(shù)學(xué)試卷

一、單項選擇題：每題只有一個選項是正確的（共8小題，每小題5分，共40分）

• 1．已知直線l₁的方程為2x+（5+m）y=8，直線l₂的方程為（3+m）x+4y=5-3m,若l₁∥l₂，則m=（　　）

  A．-1或-7

  B．-1

  C．-7

  D．-3
  組卷：290引用：5難度：0.7

  解析

• 2．M是拋物線y²=2x上一點，F(xiàn)是拋物線的焦點，以Fx為始邊、FM為終邊的角∠xFM=60°，則|FM|=（　　）

  A．1

  B．2

  C． 3

  D．4
  組卷：151引用：5難度：0.8

  解析

• 3．某區(qū)教育局招聘了8名教師，平均分配給兩個學(xué)校，其中2名語文教師不能分配在同一個學(xué)校，另外3名數(shù)學(xué)教師也不能全分配在同一個學(xué)校，則不同的分配方案共有（　　）

  A．18種

  B．24種

  C．36種

  D．48種
  組卷：145引用：1難度：0.8

  解析

• 4．101¹⁰被9除的余數(shù)為（　　）

  A．5

  B．6

  C．7

  D．8
  組卷：38引用：1難度：0.7

  解析

• 5．托馬斯?貝葉斯（Thomas Bayes）在研究“逆向概率”的問題中得到了一個公式：P（A|B）=

  P

  （

  B

  |

  A

  ）

  ?

  P

  （

  A

  ）

  P

  （

  B

  |

  A

  ）

  ?

  P

  （

  A

  ）

  +

  P

  （

  B

  |

  A

  c

  ）

  ?

  P

  （

  A

  c

  ）

  ，這個公式被稱為貝葉斯公式（貝葉斯定理），其中P（B|A）?P（A）+P（B|A^c）?P（A^c）稱為B的全概率．這個定理在實際生活中有著重要的應(yīng)用價值．假設(shè)某種疾病在所有人群中的感染率是0.1%，醫(yī)院現(xiàn)有的技術(shù)對于該疾病檢測準(zhǔn)確率為99%，即已知患病情況下，99%的可能性可以檢查出陽性，正常人99%的可能性檢查為正常．如果從人群中隨機(jī)抽一個人去檢測，經(jīng)計算檢測結(jié)果為陽性的全概率為0.01098，請你用貝葉斯公式估計在醫(yī)院給出的檢測結(jié)果為陽性的條件下這個人得病的概率（　　）

  A．0.1%

  B．8%

  C．9%

  D．99%
  組卷：1090引用：3難度：0.7

  解析

• 6．已知橢圓

  E

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的右焦點F與拋物線y²=12x的焦點重合，過點F的直線交E于A、B兩點，若AB的中點坐標(biāo)為（1，-1），則E的方程為（　　）

  A． x 2 45 + y 2 36 = 1	B． x 2 36 + y 2 27 = 1
  C． x 2 27 + y 2 18 = 1	D． x 2 18 + y 2 9 = 1
  組卷：190引用：2難度：0.6

  解析

• 7．在平面直角坐標(biāo)系中，已知點A（-1，0），B（2，0），圓

  C

  ：

  （

  x

  -

  2

  ）

  2

  +

  （

  y

  -

  m

  ）

  2

  =

  1

  4

  （

  m

  ＞

  0

  ）

  ，在圓上存在點P滿足|PA|=2|PB|，則實數(shù)m的取值范圍是（　　）

  A． [ 2 2 ， 6 2 ]

  B． [ 5 4 ， 21 2 ]

  C． （ 0 ， 21 2 ]

  D． [ 5 2 ， 21 2 ]
  組卷：400引用：10難度：0.5

  解析

四、解答題

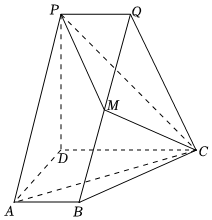• 21．如圖PD⊥平面ABCD，AD⊥CD，AB∥CD，PQ∥CD，AD=CD=DP=2PQ=2AB=2，點M為BQ的中點．
  （1）求二面角Q-PM-C的正弦值；
  （2）若N為線段CQ上的點，且直線DN與平面PMQ所成的角為

  π

  6

  ，求線段QN的長．
  組卷：87引用：5難度：0.4

  解析

• 22．已知，橢圓C過點A（

  3

  2

  ，

  5

  2

  ），兩個焦點為（0，2），（0，-2），E，F(xiàn)是橢圓C上的兩個動點，直線AE的斜率與AF的斜率互為相反數(shù)．
  （1）求橢圓C的方程；
  （2）求證：直線EF的斜率為定值．
  組卷：98引用：4難度：0.5

  解析