當前位置：試卷中心 > 試卷詳情

2021-2022學年江蘇省蘇州中學高一（下）期末數學試卷

發布：2024/7/1 8:0:9

1．已知i為虛數單位，復數z滿足（1-i）z=i,則在復平面內表示復數z的點所在的象限為（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
組卷：26引用：1難度：0.7
解析
2．若數據b₁，b₂，b₃，b₄的方差為2，則數據2b₁+3，2b₂+3，2b₃+3，2b₄+3的方差是（　　）
A．6 B．8 C．7 D．12
組卷：44引用：1難度：0.9
解析
3．在△ABC中，D為BC的中點，E為AB上一點，則
AB
+
AC
-
2
AE
=（　　）
A．
0
B．
ED
C．
DE
D．
2
ED
組卷：551引用：5難度：0.7
解析
4．設α，β是兩個不同的平面，m是直線且m?α，“m∥β”是“α∥β”的（　　）
A．充分而不必要條件 B．必要而不充分條件
C．充分必要條件 D．既不充分也不必要條件
組卷：3107引用：67難度：0.9
解析
5．在△ABC中，
AB
=
2
，
∠
C
=
π
3
，則AC+BC的最大值為（　　）
A．2 B．3 C．4 D．5
組卷：173引用：2難度：0.8
解析
6．在△ABC中，設
AC
2
-
AB
2
=
2
AM
?
BC
，那么動點M的軌跡必通過△ABC的（　　）
A．垂心 B．內心 C．外心 D．重心
組卷：201引用：6難度：0.7
解析
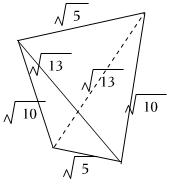7．一個相對棱長都相等的四面體，通常稱之為等腰四面體（如圖），其三組對棱長分加為
5
，
1
0
，
13
，則此四面體外接球的表面積為（　　）
A．14π B．28π
C．56π D．以上答案都不正確
組卷：95引用：1難度：0.6
解析

21．如圖1，在△ABC中，AB=BC=2，∠B=
2
3
π，E為AC的中點，現將△ABC及其內部以邊AB為軸進行旋轉，得到如圖2所示的新的幾何體，點O為C旋轉過程中形成的圓的圓心（點O即為頂點A在底面的射影），C′為圓O上任意一點．
?
（1）求新的何體的體積；
（2）記EC′與底面OCC′所成角為θ．
①求sinθ的取值范圍；
②當sinθ=
6
4
時，求證：平面ACO⊥平面AC′O．
組卷：75引用：1難度：0.5
解析
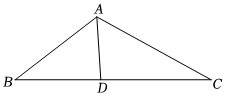22．若可變形的三角形模型在變換過程中三角形周長和面積可同時取得最小值（或最大值），則稱此模型為“周積三角形”．某模型廠家用一根定長連接桿AD，兩根單向伸縮連接桿AB、AC（A端固定，B、C端可伸縮）以及一根雙向伸縮連接桿BC制作了如圖所示的可變三角形模型（所有連接桿均為筆直的金屬桿）．模型中，雙向伸縮桿BC用一個活動連接裝置固定在D點，使BC可在D處自由轉動．已知：模型中，∠BAD=∠CAD=60°，AD=1分米，AB和AC最多可伸長到5分米，BC的雙向伸縮能力均很強．設AB=x分米，AC=y分米．
（1）將y表示成x的函數，并求其定義域；
（2）判斷此模型是否為“周積三角形”模型，并說明理由．
組卷：79引用：2難度：0.5
解析