2022-2023學年廣東省深圳市南山外國語學校（集團）高級中學高二（上）期中數學試卷

一、選擇題（本題共8小題，每小題5分，共40分。每小題給出的選項中只有一項符合題目要求）

• 1．若直線l₁：mx-y-4=0與l₂：x+2y+3=0平行，則實數m=（　　）

  A．2

  B．-2

  C． - 1 2

  D． 1 2
  組卷：134引用：4難度：0.8

  解析

• 2．拋物線

  y

  =

  -

  1

  8

  x

  2

  的準線方程是（　　）

  A． x = 1 32

  B．y=2

  C． y = 1 32

  D．y=-2
  組卷：275引用：4難度：0.8

  解析

• 3．雙曲線

  y

  2

  a

  2

  -

  x

  2

  =1的實軸長為4，則其漸近線方程為（　　）

  A．x±4y=0

  B．4x±y=0

  C．x±2y=0

  D．2x±y=0
  組卷：418引用：6難度：0.9

  解析

• 4．已知

  a

  =

  （

  1

  ，

  1

  ，

  1

  ）

  為平面α的一個法向量，A（1，0，0）為α內的一點，則點D（1，1，2）到平面α的距離為（　　）

  A． 3

  B． 2

  C． 5 2

  D． 6 3
  組卷：232引用：11難度：0.7

  解析

• 5．阿波羅尼斯（約公元前262-190年）證明過這樣一個命題：平面內到兩定點距離之比為常數k（k＞0，k≠1）的點的軌跡是圓，后人將這個圓稱為阿氏圓．若平面內兩定點A（-1，0），B（1，0），動點P滿足

  |

  PA

  |

  |

  PB

  |

  =

  2

  ，當P、A、B不共線時，△PAB面積的最大值是（　　）

  A．4

  B．2

  C． 2 3

  D． 4 3
  組卷：98引用：3難度：0.7

  解析

• 6．設橢圓

  x

  2

  25

  +

  y

  2

  16

  =1的左、右焦點分別為F₁，F₂，點P在橢圓上，且滿足

  PF

  1

  ?

  P

  F

  2

  =9，則|PF₁|?|PF₂|的值是（　　）

  A．14

  B．17

  C．20

  D．23
  組卷：435引用：3難度：0.6

  解析

• 7．已知點A（3，-1），B（5，-2），且點P在直線x+y=0上，若使|PA|+|PB|取得最小值，則點P的坐標為（　　）

  A． （ 13 5 ，- 13 5 ）

  B． （ 12 5 ，- 12 5 ）

  C．（-2，2）

  D．（2，-2）
  組卷：257引用：2難度：0.7

  解析

四、解答題（本題共6小題，共70分。解答題應寫出文字說明、證明過程或演算步驟）

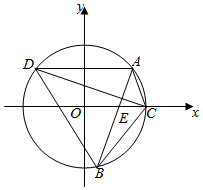• 21．如圖，過點E（1，0）的直線與圓O：x²+y²=4相交于A、B兩點，過點C（2，0）且與AB垂直的直線與圓O的另一交點為D．
  （1）當點B坐標為（0，-2）時，求直線CD的方程；
  （2）求四邊形ABCD面積S的最大值．
  組卷：284引用：10難度：0.5

  解析

• 22．已知雙曲線C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  過點

  （

  2

  ，

  2

  ）

  ，且漸近線方程為y=±2x.直線l過點（0，1），且與C交于M，N兩點．
  （1）求雙曲線C的方程；
  （2）在y軸上是否存在定點Q，使得

  QM

  ?

  QN

  為定值？若存在，求出點Q坐標；若不存在，說明理由．
  組卷：153引用：2難度：0.6

  解析