2014-2015學(xué)年福建省泉州市南安一中高二（上）國(guó)慶檢測(cè)數(shù)學(xué)試卷

一、選擇題（本大題共12個(gè)小題，每小題5分，共60分，在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符號(hào)題目要求）

• 1．命題“所有能被2整除的整數(shù)都是偶數(shù)”的否定是（　　）

  A．所有不能被2整除的整數(shù)都是偶數(shù)

  B．所有能被2整除的整數(shù)都不是偶數(shù)

  C．存在一個(gè)不能被2整除的整數(shù)是偶數(shù)

  D．存在一個(gè)能被2整除的整數(shù)不是偶數(shù)
  組卷：1045引用：118難度：0.9

  解析

• 2．動(dòng)點(diǎn)P到點(diǎn)M（1，0）與點(diǎn)N（3，0）的距離之差為2，則點(diǎn)P的軌跡是（　　）

  A．雙曲線	B．雙曲線的一支
  C．兩條射線	D．一條射線
  組卷：196引用：50難度：0.7

  解析

• 3．拋物線y²=10x的焦點(diǎn)到準(zhǔn)線的距離是（　　）

  A． 5 2

  B．5

  C． 15 2

  D．10
  組卷：183引用：67難度：0.9

  解析

• 4．已知命題p：?n∈N，2ⁿ＞1000，則￢p為（　　）

  A．?n∈N，2n≤1000	B．?n∈N，2n＞1000
  C．?n∈N，2n≤1000	D．?n∈N，2n＜1000
  組卷：432引用：57難度：0.9

  解析

• 5．若橢圓的對(duì)稱軸為坐標(biāo)軸，長(zhǎng)軸長(zhǎng)與短軸長(zhǎng)的和為18，焦距為6，則橢圓的方程為（　　）

  A． x 2 9 + y 2 16 = 1

  B． x 2 25 + y 2 16 = 1

  C． x 2 25 + y 2 16 = 1 或 x 2 16 + y 2 25 = 1

  D．以上都不對(duì)
  組卷：553引用：41難度：0.9

  解析

• 6．“a=2”是“直線2x+ay-1=0與直線ax+2y-2=0平行”的（　　）

  A．充要條件	B．充分不必要條件
  C．必要不充分條件	D．既不充分也不必要條件
  組卷：104引用：12難度：0.9

  解析

• 7．設(shè)雙曲線

  y

  2

  m

  -

  x

  2

  2

  =

  1

  的一個(gè)焦點(diǎn)為（0，-2），則雙曲線的離心率為（　　）

  A． 2

  B．2

  C． 6

  D． 2 2
  組卷：7引用：3難度：0.9

  解析

三、解答題（本大題共6個(gè)小題，共74分，解答應(yīng)寫出文字說明，證明過程或演算步驟）

• 21．已知橢圓

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的兩個(gè)焦點(diǎn)為F₁，F(xiàn)₂，橢圓上一點(diǎn)M（

  2

  6

  3

  ，

  3

  3

  ）滿足

  M

  F

  1

  ?

  M

  F

  2

  =0．
  （Ⅰ）求橢圓的方程；
  （Ⅱ）若直線l：y=kx+

  2

  與橢圓有不同交點(diǎn)A，B，且

  OA

  ?

  OB

  ＞1（O為坐標(biāo)原點(diǎn)），求實(shí)數(shù)k的取值范圍．
  組卷：221引用：9難度：0.5

  解析

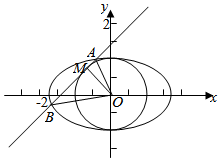• 22．如圖，在由圓O：x²+y²=1和橢圓C：

  x

  2

  a

  2

  +

  y

  2

  =1（a＞1）構(gòu)成的“眼形”結(jié)構(gòu)中，已知橢圓的離心率為

  6

  3

  ，直線l與圓O相切于點(diǎn)M，與橢圓C相交于兩點(diǎn)A，B．
  （1）求橢圓C的方程；
  （2）是否存在直線l,使得

  OA

  ?

  OB

  =

  1

  2

  OM

  2

  ，若存在，求此時(shí)直線l的方程；若不存在，請(qǐng)說明理由．
  組卷：22引用：9難度：0.3

  解析