2022-2023學(xué)年湖南省張家界市高一（下）期末數(shù)學(xué)試卷

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知z=2-i,則z（

  z

  +i）=（　　）

  A．6-2i

  B．4-2i

  C．6+2i

  D．4+2i
  組卷：5178引用：47難度：0.9

  解析

• 2．運(yùn)動員甲10次射擊成績（單位：環(huán)）如下：7，8，9，7，4，8，9，9，7，2，則下列關(guān)于這組數(shù)據(jù)說法不正確的是（　　）

  A．眾數(shù)為7和9	B．平均數(shù)為7
  C．中位數(shù)為7	D．方差為s2=4.8
  組卷：287引用：8難度：0.8

  解析

• 3．目前，甲型流感病毒在國內(nèi)傳播，據(jù)某市衛(wèi)健委通報，該市流行的甲型流感病毒，以甲型H1N1亞型病毒為主，假如該市某小區(qū)共有100名感染者，其中有10名年輕人，60名老年人，30名兒童，現(xiàn)用分層抽樣的方法從中隨機(jī)抽取20人進(jìn)行檢測，則做檢測的老年人人數(shù)為（　　）

  A．6

  B．10

  C．12

  D．16
  組卷：289引用：3難度：0.9

  解析

• 4．已知某圓錐的母線長為4，高為

  2

  3

  ，則圓錐的全面積為（　　）

  A．10π

  B．12π

  C．14π

  D．16π
  組卷：253引用：4難度：0.8

  解析

• 5．某校從高一新生中隨機(jī)抽取了一個容量為10的身高樣本，數(shù)據(jù)（單位：cm）從小到大排序下：158，165，165，167，168，169，x,172，173，175．若樣本數(shù)據(jù)的第60百分位數(shù)是170，則x=（　　）

  A．169

  B．170

  C．171

  D．172
  組卷：237引用：5難度：0.8

  解析

• 6．已知向量

  a

  ，

  b

  滿足

  |

  a

  |

  =

  2

  ，

  |

  b

  |

  =

  3

  ，

  a

  ?

  b

  =

  1

  ，則

  b

  在

  a

  上的投影向量為（　　）

  A． - 1 4 a

  B． - 1 9 a

  C． 1 4 a

  D． 1 9 a
  組卷：98引用：6難度：0.7

  解析

• 7．張益唐是當(dāng)代著名華人數(shù)學(xué)家．他在數(shù)論研究方面取得了巨大成就，曾經(jīng)在《數(shù)學(xué)年刊》發(fā)表《質(zhì)數(shù)間的有界間隔》，證明了存在無窮多對質(zhì)數(shù)間隙都小于7000萬.2013年張益唐證明了孿生素數(shù)猜想的一個弱化形式．孿生素數(shù)猜想是希爾伯特在1900年提出的23個問題之一，可以這樣描述：存在無窮多個素數(shù)p,使得p+2是素數(shù)，素數(shù)對（p,p+2）稱為孿生素數(shù)．在不超過12的素數(shù)中，隨機(jī)選取兩個不同的數(shù)，能夠組成孿生素數(shù)的概率是（　　）

  A． 1 4

  B． 1 5

  C． 1 10

  D． 1 20
  組卷：75引用：3難度：0.7

  解析

四、解答題：本題共6小題，共70分.解答應(yīng)寫出文字說明、證明過程或演算步驟.

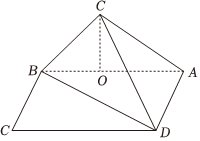• 21．如圖，在矩形ABCD中，

  AB

  =

  3

  ，

  BC

  =

  1

  ，沿對角線BD把△BCD折起，使C移到C′，且C′在面ABC內(nèi)的射影O恰好落在AB上．
  （1）求證：AD⊥C′B；
  （2）求AB與平面C′BD所成的角的正弦值．
  組卷：106引用：3難度：0.5

  解析

• 22．在△ABC中，內(nèi)角A，B，C的對邊分別為a,b,c,且

  1

  tan

  B

  +

  1

  tan

  C

  =

  1

  tan

  A

  ．
  （1）求

  b

  2

  +

  c

  2

  a

  2

  的值；
  （2）記△ABC的面積為S，點(diǎn)P是△ABC內(nèi)一點(diǎn)，且∠PAB=∠PBC=∠PCA=θ，證明：
  ①

  tan

  A

  =

  4

  S

  b

  2

  +

  c

  2

  -

  a

  2

  ；
  ②tanA=2tanθ．
  組卷：45引用：2難度：0.6

  解析