2022-2023學年黑龍江省哈爾濱市尚志中學高三(上)期中數學試卷
發布:2024/10/31 14:0:2
一、單選題(每小題5分)
-
1.已知全集
,集合A={x∈N|2≤2x≤8},則?UA=( )U={x∈N|0≤log2x≤1}A.{x|3<x≤4} B.{4} C.{0,4} D.{x|3≤x≤4} 組卷:29引用:3難度:0.8 -
2.復數z滿足(3-4i)?z=|4+3i|,則
=( )zA. i35-45B. i35+45C.- i45+35D.- i35+45組卷:196引用:7難度:0.8 -
3.函數
定義域為R的一個充分不必要條件是( )f(x)=mx2+2x+2A. m≥13B. m≥14C. m≥23D. m≥12組卷:61引用:3難度:0.7 -
4.已知定義在R上的偶函數f(x)滿足f(1-x)=f(3+x),且當x∈[0,2]時,f(x)=
,則f(-2023)=( )2x+1,0≤x<1log2(x+3),1≤x≤2A.log26 B.1 C.2 D.3 組卷:18引用:3難度:0.7 -
5.設等比數列{an}的公比為q,其前n項和為Sn,前n項積為Tn,且滿足條件a1>1,a2020a2021>1,(a2020-1)(a2021-1)<0,則下列選項錯誤的是( )
A.0<q<1 B.S2020+1>S2021 C.T2020是數列{Tn}中的最大項 D.T4041>1 組卷:54引用:2難度:0.6 -
6.四面體ABCD的四個頂點都在球O的球面上,AB=AD=CD=2,
,BD⊥CD,平面ABD⊥平面BCD,則球O的體積為( )BD=22A. 42πB. 32πC. 43πD.2π 組卷:89引用:3難度:0.5 -
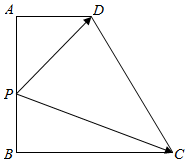 7.如圖,在直角梯形ABCD中,AD∥BC,AB⊥BC、AD=2.BC=3,P是線段AB上的動點,
7.如圖,在直角梯形ABCD中,AD∥BC,AB⊥BC、AD=2.BC=3,P是線段AB上的動點,
則||的最小值為( )PC+2PDA.2 5B.5 C.3 5D.7 組卷:643引用:5難度:0.4
四、解答題(17題10分,其余題每題12分)
-
21.已知橢圓E:
的離心率為x2a2+y2b2=1(a>b>0),右焦點為F,點63,直線FG與圓Q:G(0,6)相切.(x-6)2+(y-6)2=3
(1)求直線FG和橢圓E的方程;
(2)直線FG與橢圓E交于A,B兩點,C,D為橢圓E上的兩點,若四邊形CADB的對角線CD⊥AB,求四邊形CADB的面積的最大值.組卷:22引用:4難度:0.5 -
22.已知函數f(x)=x-lnx-2.
(1)求曲線y=f(x)在x=1處的切線方程;
(2)記函數g(x)=x2-bx-2-f(x),設x1,x2(x1<x2)是函數g(x)的兩個極值點,若b≥12,且g(x1)-g(x2)≥k恒成立,求實數k的最大值.32組卷:41引用:3難度:0.5


