2022-2023學年重慶市南開中學高一（上）質檢數學試卷（線上）

一、選擇題：本大題8個小題，每小題5分，共40分，每小題只有一個選項符合要求，答案請涂寫在機讀卡上.

• 1．設集合M={0，1，2，4}，N={x|2≤2^x≤8}，則M∩N=（　　）

  A．?

  B．{1，2}

  C．{0，1，2}

  D．{x|1≤x≤3}
  組卷：45引用：3難度：0.9

  解析

• 2．已知冪函數y=f（x）的圖象經過點（2，4），則f（

  2

  ）的值為（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：57引用：3難度：0.8

  解析

• 3．“x＜0”是“x（x-2）＞0”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：16引用：2難度：0.9

  解析

• 4．函數

  f

  （

  x

  ）

  =

  2

  x

  x

  2

  +

  1

  的圖象大致為（　　）

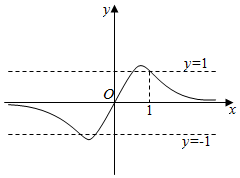
  A．	B．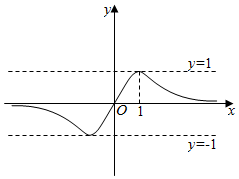
  C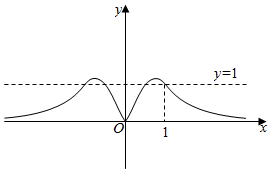．	D．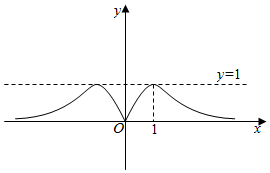
  組卷：127引用：16難度：0.8

  解析

• 5．若

  a

  =

  2

  2

  ，b=2^0.3，c=0.9^3.1，則（　　）

  A．b＞c＞a

  B．b＞a＞c

  C．c＞a＞b

  D．a＞b＞c
  組卷：293引用：3難度：0.7

  解析

• 6．函數

  f

  （

  x

  ）

  =

  2

  x

  2

  -

  7

  x

  +

  3

  的單調遞減區間為（　　）

  A． （ - ∞ ， 7 4 ）

  B． （ - ∞ ， 1 2 ）

  C． （ 7 4 ， + ∞ ）

  D．（3，+∞）
  組卷：217引用：2難度：0.7

  解析

• 7．已知函數f（x）為奇函數，且在區間（0，+∞）上是增函數，若

  f

  （

  1

  2

  ）

  =

  0

  ，則

  f

  （

  x

  ）

  x

  ≤

  0

  的解集是（　　）

  A． （ - ∞ ，- 1 2 ] ∪ （ 0 ， 1 2 ]	B． [ - 1 2 ， 0 ） ∪ （ 0 ， 1 2 ]
  C． （ - ∞ ，- 1 2 ） ∪ （ 1 2 ， + ∞ ）	D． [ 1 2 ， + ∞ ）
  組卷：111引用：2難度：0.7

  解析

四、解答題：本大題6個小題，共70分.各題解答必須答在答題卡上（必須寫出必要的文字說明、演算步驟或推理過程）.

• 21．已知函數

  f

  （

  x

  ）

  =

  1

  -

  a

  5

  x

  +

  1

  為奇函數．
  （1）求實數a的值；
  （2）設g（x）=f（x）+x,直接判斷g（x）的單調性（不需證明）；
  （3）若?m∈[-1，1]，不等式f（x²）+f（mx-2）≤2-x²-mx恒成立，求實數x的取值范圍．
  組卷：30引用：1難度：0.6

  解析

• 22．定義在（-1，1）上的函數f（x）滿足：對任意的x,y∈（-1，1），都有

  f

  （

  x

  ）

  +

  f

  （

  y

  ）

  =

  f

  （

  x

  +

  y

  1

  +

  xy

  ）

  ，且當x∈（-1，0），f（x）＞0．
  （1）求證：函數f（x）是奇函數；
  （2）求證：f（x）在（-1，1）上是減函數；
  （3）解不等式：

  f

  （

  x

  +

  1

  ）

  +

  f

  （

  1

  1

  -

  x

  ）

  ＞

  0

  ；
  （4）求證：

  f

  （

  1

  5

  ）

  +

  f

  （

  1

  11

  ）

  +

  …

  +

  f

  （

  1

  n

  2

  +

  3

  n

  +

  1

  ）

  ＞

  f

  （

  1

  2

  ）

  ．
  組卷：149引用：5難度：0.4

  解析