2020-2021學年江蘇省揚州中學高二(下)開學數學試卷
發布:2024/4/20 14:35:0
一、單項選擇題(本大題共8小題,每小題5分,共40分.在每小題給出的四個選項中,只有一項符合要求).
-
1.“x=1”是“x2=1”的( )
A.充分而不必要條件 B.必要而不充分條件 C.充分必要條件 D.既不充分也不必要條件 組卷:719引用:21難度:0.9 -
2.已知雙曲線C與雙曲線
有相同的焦點,且其中一條漸近線方程為y=-2x,則雙曲線C的標準方程是( )y23-x22=1A. y24-x23=1B. y22-x2=1C. y28-x22=1D. y24-x2=1組卷:119引用:4難度:0.6 -
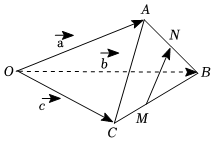 3.如圖,設,OA=a,OB=b,若OC=c,AN=NB,則BM=2MC=( )MN
3.如圖,設,OA=a,OB=b,若OC=c,AN=NB,則BM=2MC=( )MNA. 12a+16b-23cB. -12a-16b+23cC. 12a-16b-13cD. -12a+16b+13c組卷:163引用:10難度:0.7 -
4.《萊茵德紙草書》是世界上最古老的數學著作之一.書中有一道這樣的題目:把100個面包分給5個人,使每人所得成等差數列,且使較大的三份之和的
是較小的兩份之和,則最大的一份為( )17A. 1153B. 1183C. 1213D. 1243組卷:283引用:8難度:0.7 -
5.在正方體ABCD-A1B1C1D1中,E是C1C的中點,則直線BE與平面B1BD所成的角的正弦值為( )
A.- 105B. 105C.- 155D. 155組卷:829引用:21難度:0.7 -
6.不等式(a2-9)x2+(a+3)x-1≥0的解集是空集,則實數a的范圍為( )
A.(-3, )95B.[-3, )95C.[-3, ]95D.[-3, )∪{3}95組卷:563引用:4難度:0.7 -
7.已知數列{an}滿足a1=1,an+1-an=an2,若數列{an2}的前50項和為m,則數列{
}的前50項和為( )1an+1A. 2m1+mB. m1+mC. m-1mD. m-12m組卷:318引用:3難度:0.4
四、解答題(本大題共6小題,計70分.應寫出必要的文字說明、證明過程或演算步驟)
-
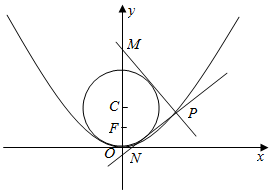 21.已知拋物線E:x2=2py(0<p<2)的焦點為F,圓C:x2+(y-1)2=1,點P(x0,y0)為拋物線上一動點.當|PF|=時,△PFC的面積為5p2.12
21.已知拋物線E:x2=2py(0<p<2)的焦點為F,圓C:x2+(y-1)2=1,點P(x0,y0)為拋物線上一動點.當|PF|=時,△PFC的面積為5p2.12
(1)求拋物線E的方程;
(2)若y0>,過點P作圓C的兩條切線分別交y軸于M,N兩點,求△PMN面積的最小值,并求出此時點P的坐標.12組卷:1090引用:8難度:0.1 -
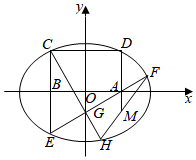 22.如圖,已知橢圓,矩形ABCD的頂點A,B在x軸上,C,D在橢圓Γ上,點D在第一象限.CB的延長線交橢圓Γ于點E,直線AE與橢圓Γ、y軸分別交于點F、G,直線CG交橢圓Γ于點H,DA的延長線交FH于點M.Γ:x24+y22=1
22.如圖,已知橢圓,矩形ABCD的頂點A,B在x軸上,C,D在橢圓Γ上,點D在第一象限.CB的延長線交橢圓Γ于點E,直線AE與橢圓Γ、y軸分別交于點F、G,直線CG交橢圓Γ于點H,DA的延長線交FH于點M.Γ:x24+y22=1
(1)設直線AE、CG的斜率分別為k1、k2,求證:為定值;k1k2
(2)求直線FH的斜率k的最小值;
(3)證明:動點M在一個定曲線上運動.組卷:154引用:3難度:0.3


