當前位置：試卷中心 > 試卷詳情

2020-2021學年北京四中高三（下）開學數學試卷

發布：2024/12/14 23:0:1

1．已知集合A={x|-1≤x＜3}，B={x∈Z|x²＜4}，則A∩B=（　　）
A．{0，1} B．{-1，0，1}
C．{-1，0，1，2} D．{-2，-1，0，1，2}
組卷：73引用：9難度：0.9
解析
2．已知復數z滿足z+|z|=3+i,則z=（　　）
A．1-i B．1+i C．
4
3
-i D．
4
3
+i
組卷：127引用：4難度：0.8
解析
3．設{a_n}為等差數列，a₁=22，S_n為其前n項和，若S₁₀=S₁₃，則公差d=（　　）
A．-2 B．-1 C．1 D．2
組卷：225引用：4難度：0.9
解析
4．函數y=lncosx（-
π
2
＜x＜
π
2
）的大致圖象是（　　）
A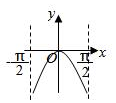． B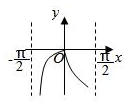． C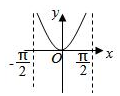． D．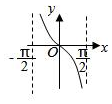
組卷：117引用：4難度：0.9
解析
5．已知向量
a
=（1，1），4
a
+
b
=（4，2），則向量
a
與
b
的夾角為（　　）
A．
π
4
B．
π
3
C．
2
π
3
D．
3
π
4
組卷：115引用：3難度：0.5
解析
6．從0，2中選一個數字，從1，3，5中選兩個數字，組成無重復數字的三位數，則這個數是奇數的概率為（　　）
A．
1
2
B．
3
5
C．
2
5
D．
3
4
組卷：100引用：2難度：0.7
解析
7．已知函數f（x）=
2
x
，
x
≥
a
-
x
,
x
＜
a
，若函數f（x）存在零點，則實數a的取值范圍是（　　）
A．（-∞，0） B．（-∞，1） C．（1，+∞） D．（0，+∞）
組卷：444引用：5難度：0.7
解析

20．已知函數，f（x）=x²（x＞0），g（x）=alnx（a＞0）．
（Ⅰ）若f（x）＞g（x）恒成立，求實數a的取值范圍；
（Ⅱ）當a=1時，過f（x）上一點（1，1）作g（x）的切線，判斷：可以作出多少條切線，并說明理由．
組卷：396引用：4難度：0.2
解析
21．已知項數為m（m∈N^*，m≥2）的數列{a_n}滿足如下條件：①a_n∈N^*（n=1，2，…，m）；②a₁＜a₂＜…＜a_m．若數列{b_n}滿足b_n=
（
a
1
+
a
2
+
…
+
a
m
）
-
a
n
m
-
1
∈
N
*
，其中n=1，2，…，m,則稱{b_n}為{a_n}的“伴隨數列”．
（Ⅰ）數列1，3，5，7，9是否存在“伴隨數列”，若存在，寫出其“伴隨數列”；若不存在，請說明理由；
（Ⅱ）若{b_n}為{a_n}的“伴隨數列”，證明：b₁＞b₂＞…＞b_m；
（Ⅲ）已知數列{a_n}存在“伴隨數列”{b_n}，且a₁=1，a_m=2049，求m的最大值．
組卷：232引用：8難度：0.2
解析