2022-2023學年江西省贛州市教育發展聯盟高三（上）第九次聯考數學試卷（文科）（12月份）

一、選擇題:本大題共12小題，每小題5分,共60分。在每小題給出的四個選項中,只有一項是符合題目要求的。

• 1．已知集合A={x|（x-2）（2x+1）≤0}，B={x|x＜1}，則A∩B=（　　）

  A．{x|- 1 2 ≤ x ≤ 1 }

  B．{x|- 1 2 ≤ x ＜ 1 }

  C．{x|1≤x≤2}

  D．{x|x ≤ - 1 2 }
  組卷：82引用：4難度：0.8

  解析

• 2．“α∈（0，

  π

  2

  ）”是“tanα＞0”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：74引用：5難度：0.8

  解析

• 3．已知函數f（x）=

  m

  ?

  2

  x

  -

  1

  2

  x

  +

  1

  （m∈R）是奇函數，則m=（　　）

  A．0

  B．1

  C．-1

  D．±1
  組卷：203引用：3難度：0.8

  解析

• 4．斐波那契數列{a_n}可以用如下方法定義：a_n+2=a_n+1+a_n，且a₁=a₂=1，若此數列各項除以4的余數依次構成一個新數列{b_n}，則數列{b_n}的第100項為（　　）

  A．0

  B．1

  C．2

  D．3
  組卷：27引用：1難度：0.7

  解析

• 5．若實數x,y滿足

  x - 2 y ≤ 0

  2 x + y + 4 ≥ 0

  y ≤ 1

  ，則z=3x+2y的最大值為（　　）

  A．8

  B．6

  C． 32 5

  D．- 11 2
  組卷：73引用：6難度：0.7

  解析

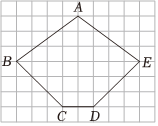• 6．如圖中小正方形的邊長為1，粗線畫出的是某平面多邊形，現將該圖形繞對稱軸旋轉180°，則所得幾何體的體積為（　　）

  A．35π

  B．36π

  C．37π

  D．39π
  組卷：3引用：1難度：0.7

  解析

• 7．若函數

  f

  （

  x

  ）

  =

  2

  cos

  （

  ωx

  +

  π

  4

  ）

  （

  ω

  ＞

  0

  ）

  在

  （

  0

  ，

  7

  π

  4

  ）

  上單調遞減，則ω的最大值為（　　）

  A． 3 7

  B． 3 4

  C． 1 4

  D．1
  組卷：216引用：4難度：0.7

  解析

三、解答題:共70分。解答應寫出文字說明,證明過程或演算步驟。

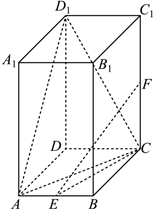• 21．如圖，在直棱柱ABCD-A₁B₁C₁D₁中，底面四邊形ABCD為邊長為

  5

  的菱形，AA₁=AC=4，E為AB的中點，F為CC₁的中點．
  （1）證明：EF∥平面ACD₁；
  （2）若點P為線段EF上的動點，求點P到平面ACD₁的距離．
  組卷：73引用：5難度：0.5

  解析

• 22．已知函數f（x）=2lnx+2ax-ax²（a∈R）．
  （1）若a=

  3

  2

  ，求曲線y=f（x）在點（1，f（1））處的切線方程；
  （2）若f′（x）是f（x）的導函數，f'（x₁）=f′（x₂）=0，且x₁＞x₂＞0，若

  f

  （

  x

  1

  ）

  +

  f

  （

  x

  2

  ）

  2

  +x₁x₂＜λ恒成立，求實數λ的取值范圍．
  組卷：18引用：1難度：0.4

  解析